by Emir Karavelić (Univ. of Sarajevo), Hermann G. Matthies (TU Braunschweig) and Adnan Ibrahimbegovic (Univ. de Technologie de Compiègne)
Bayesian inference can be used in machine learning to provide a reduced order model for multi-scale stochastic plasticity, with parameters as random variables. Machine learning can deliver either the random variables or their probability measure.
We are developing a machine learning procedure that provides a probability-based scale bridging for concrete composite material. This method is appropriate for situations in which the scale separation of standard homogenisation approach does not apply. The proposed procedure is capable of passing the detailed information available at the micro-scale (at which different phases are visible) to the chosen reduced order model at the macro-scale (where concrete is a single continuum). This is accomplished, not only for representing elastic, but also different phases of inelastic response, resulting in a stochastic plasticity model for localised failure. This proposed machine learning procedure exploits Bayesian inference to provide the probability distributions of such stochastic plasticity model parameters expressed as random variables (RV). Two different approaches of Bayesian inference can be used to quantify the uncertainty: one constructs the RV, the other the probability measure.
This work contributes to machine learning formalism through the development of stochastic constitutive models that capture localised failure sensitivity to initial and induced defects for structures built of heterogeneous composite material, such as concrete. Such models can enable better predictions of crack spacing and opening, which can be used to improve concrete durability. This information is relevant to many industrial applications, given that concrete is probably the most widely used material in construction and that many existing concrete structures are rapidly ageing.
When it comes to constructing predictive stochastic plasticity fracture models, this kind of composite material has favourable features: two-phase microstructure with aggregate vs. cement paste visible at micro-scale [1], non-local dimension owing to typical fracture modes of massive structures with significant contribution of the fracture process zone (FPZ), and a fabrication that is comparable to large-scale additive-manufacturing, where the complete structure is cast with the same material rather than an assembly of various components. The latter is the crucial hypothesis to make the proposed macro-scale stochastic plasticity model feasible in terms of predicting probability-distribution-based estimates of structure properties. The main novelty here is that a standard homogenisation approach no longer applies and all scales are to be treated probabilistically. Thus, our proposed approach is to capture not only the average response on the larger scale, but also the potential variability bounds. This is particularly important for the testing of heterogeneous cement-based composites, where the scales in the test specimen are generally poorly separated. In this work we focus in particular on the uncertainty propagation which allows the inelasticity to be connected at multiple scales, starting from the fine scale (here the micro-scale for concrete) where the heterogeneous composite failure mechanisms and the variability of model parameters can be captured much better by a corresponding representation of different phases (here aggregate vs. cement paste).
Our main focus in this work is on the model reduction from micro-scale to macro-scale, which defines generalised an ED-FEM in a probability framework and allows for stochastic coarse graining. This is illustrated in switching from micro-scale to macro-scale, to provide a replacement with a generalised ED-FEM once the crack pattern inside the corresponding micro-scale element is stabilised. Namely, the goal is to then replace the micro-scale computation with the corresponding stochastic macro-scale model of such an ED-FEM. We illustrate this idea on a plasticity model, where such parameters also include yield stress (for defining the fracture process zone — FPZ) and ultimate stress (for defining localised failure).
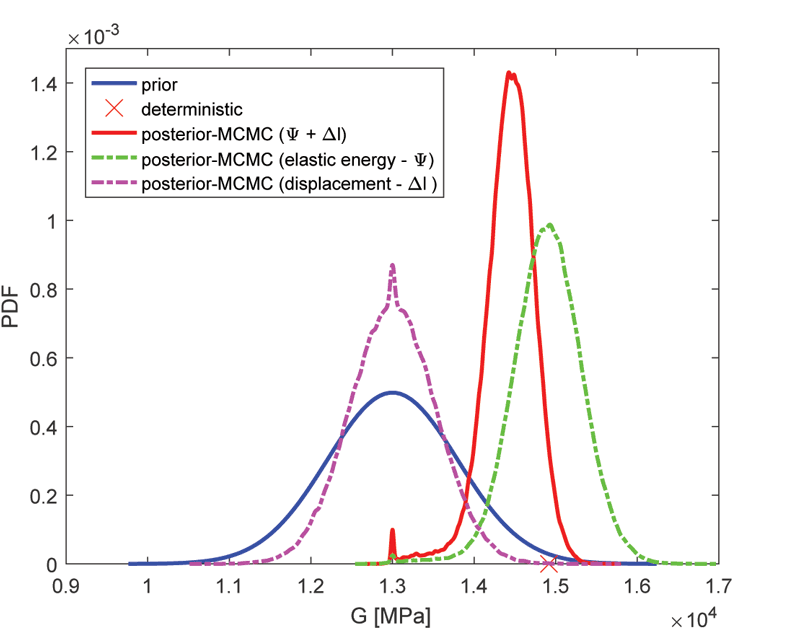
Figure 1: Comparison of prior and posterior pdf functions for shear modulus performed on uniaxial compression test obtained by MCMC (one realisation on micro-scale – w1).
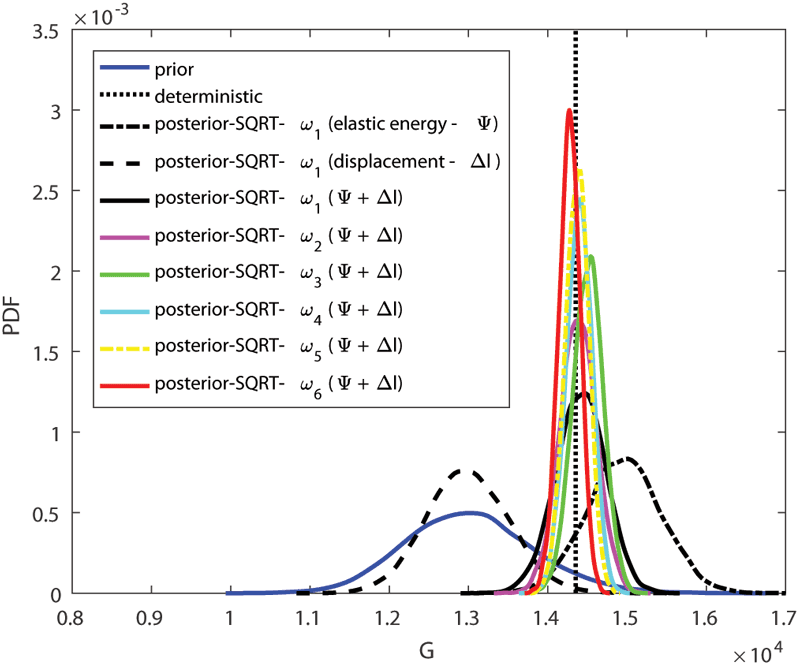
Figure 2: Comparison of prior and posterior pdf functions for shear modulus bulk modulus performed on uniaxial compression test obtained by SQRT Kalman filter (six realisations on micro-scale – w6).
Two different methods for Bayesian inference have been tested and compared in the proposed approach, both based on the Bayes theorem that makes it possible to incorporate new information that has been generated in a particular loading program. Each unknown parameter of the reduced model is modelled as a random variable. Such a description has two constituents, the measurable function representing the random variable RV, and the measure. Markov chain Monte Carlo (MCMC) updates the measure, whereas the various filters [2] change resp. update the measurable function (Figures 1 and 2). We formulate both methods as functional spectral approximations of stochastic problems and introduce, in combination with the second method, a new procedure that does not need any sampling, hence works with the subsequent update in a deterministic manner. It also seems to be the fastest and most reliable method compared with others. We show by example that the spectral resp. polynomial chaos version of the Gauss-Markov-Kalmán filter (GMKF) also works for highly nonlinear non-smooth problems with non-Gaussian measures (Figure 3 and 4). More detailed information can be found in [1,2,3].
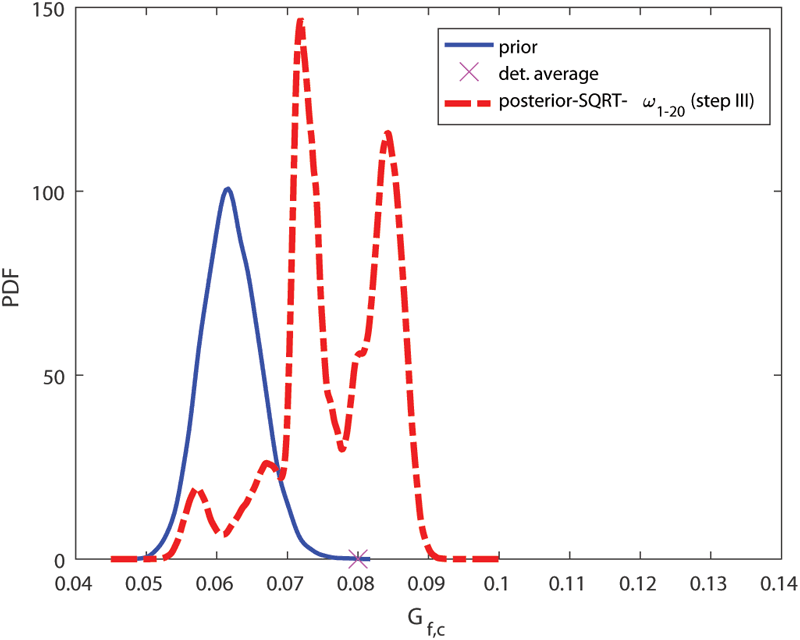
Figure 3: Updates for softening parameter Gf,c (fracture energy) obtained by SQRT Kalman filter with three measurements taken from uniaxial compression test for 20 different realisations – w20.

Figure 4: Updates for softening parameter su (limit stress) obtained by SQRT Kalman filter with three measurements taken from uniaxial compression test for 20 different realisations – w20.
References:
[1] E. Karavelić, et al.: “Concrete micro-scale model with full set of 3D failure modes with random distribution of aggregate and cement phase”, Part I: Formulation and numerical implementation, Comp. Methods Appl. Mech. Eng., 344, 1051–1072, 2019.
[2] H. G. Matthies, A. Ibrahimbegovic: “Stochastic Multiscale Coupling of Inelastic Processes in Solid Mechanics”, in: M. Papadrakakis, G. Stefanou (eds.), Multiscale Modelling and Uncertainty Quantification of Materials and Structures, 3, 135–157, (2014), Springer. doi: 10.1007/978-3-319-06331-7-9
[3] A. Ibrahimbegovic, H. G. Matthies, E. Karavelić: “Concrete micro-scale model with full set of 3D failure modes with random distribution of aggregate and cement phase”, Part II: reduced model of macro-scale stochastic plasticity identification by Bayesian inference, Comp. Methods Appl. Mech. Eng., in press, 2020.
Please contact:
Adnan Ibrahimbegovic, Universite de Technologie de Compiègne, France











