by Truong-Vinh Hoang (RWTH-Aachen University) and Hermann G. Matthies (TU Braunschweig)
Data assimilation is a challenge in many forecasting applications ranging from weather and environmental forecasting to engineering applications such as structural health monitoring and digital twins. A common technique for data assimilation is the ensemble Kalman filter (EnKF). However, it is well-known that the EnKF does not yield consistent estimates for highly nonlinear dynamical systems. Deep learning (DL) techniques can be applied to improve the EnKF in high-dimensional and nonlinear dynamical systems. This article presents an extension of the EnKF using deep neural networks (DNNs) with a focus on the theoretical and numerical aspects.
Data assimilation aims to update states of a dynamical system by combining numerical models and observed data which can be sparse in space and time. Owing to uncertainty in the numerical models as well as measurement data in the probability setting, knowledge about model states is presented using probability distributions. When new measurement data become available, the knowledge about the model states is updated by conditioning the state distribution on the measured observations, which is usually performed using Bayes’ theorem. For high-dimensional and nonlinear simulation models, an accurate representation of the assimilated state distribution comes at an extremely high computational cost. A common method for data assimilation with an acceptable computational budget is the EnKF. In this method, the state distribution is approximated by an ensemble, and the assimilation is performed by applying the Kalman filter on each ensemble’s member. It is well-known that the EnKF is not appropriate for highly nonlinear dynamical systems due to linear approximations of the dynamical systems and observation maps in the Kalman filter. Thus, there is a need to develop ensemble filtering methods that perform better in these situations.
In general, a filter is a function of the observations and the current states mapping to the assimilated states. This map can be very complex, especially for high-dimensional state spaces. Deep learning, which has significant advantages in representing complex functions between high-dimensional spaces, has great potential to be applied in these problems. Indeed, the general idea here is to use DNNs to construct filtering maps such that the assimilated ensemble approximates the conditioned distribution yielded by Bayes’ theorem. The datasets using for training the DNNs are the ensembles of states and predicted observations.
In particular, we are developing a novel DL-based ensemble conditional mean filter (EnCMF). The EnCMF is a generalisation of EnKF for nonlinear dynamical systems with non-Gaussian distributions of states and measurement errors [1]. An implementation of the EnCMF has been developed using polynomial chaos expansions for approximating the conditional expectation (CE) of mean values. However, this approximation is not suitable for high-dimensional state spaces due to the curse of dimensionality, i.e., the number of polynomials in the expansion increases exponentially with respect to dimensionality. In the DL-based EnCMF, we approximaIn the DL-based EnCMF, see Figure 1 for its implementation procedure, we approximate the CE of mean values by a DNN.te the CE of mean values by a DNN. Thanks to the orthogonal property of CE, the loss function used to train this DNN is the mean squared error—a commonly used loss criterion for DNNs. The trained DNN is then used to form the filter.
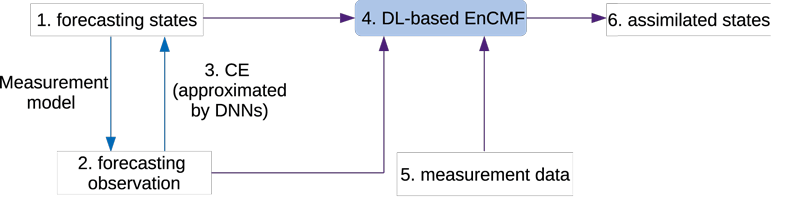
Figure 1: Implementation procedure of the DL-based EnCMF with 6 steps: (1) evaluating an ensemble of the forecasting states, (2) evaluating the corresponding ensemble of the forecasting observation, (3) approximating the CE of the mean using a DNN, (4) constructing the DL-based EnCMF, and (5, 6) plugging the measurement data into the DL-based EnCMF, and computing the assimilated ensemble.
Unlike the EnKF, the DL-based EnCMF does not linearise the dynamical system and observation maps. In comparison with the EnKF, the DL-based EnCMF yields better estimates, but it requires larger ensemble sizes. For example, by increasing the size of ensembles, the mean value of the state ensemble converges to the conditioned mean yielded by the Bayesian formulation—a property that cannot be obtained using the EnKF. A numerical challenge of the DL-EnCMF is the limit size of data sets—the ensembles of states and predicted observations—which can lead to the over-fitting problem when training DNNs. A way to ease the over-fitting phenomenon is to use techniques such as regularisation, dataset augmentation and noise robustness when training the networks.
In the future, we will investigate other DL-based filters, e.g., using conditional expectations of higher-order moments or the variational Bayesian inference. Moreover, training algorithms such as those combining online-offline training sessions to reduce the online training computational cost will be considered.
Reference:
[1] H. G. Matthies et al.: “Parameter estimation via conditional expectation: a Bayesian inversion”, Adv. Model. and Simul. in Eng. Sci. (2016) 3:24. DOI: 10.1186/s40323-016-0075-7
Please contact:
Truong Vinh Hoang, RWTH-Aachen, Germany
Herman G. Matthies, Technische Universität Braunschweig, Germany











