by Sebastian Raubitzek and Thomas Neubauer (Vienna University of Technology)
Machine learning has found its way into agricultural science for analysis and predictions, e.g., of yield or nitrogen status. Results are encouraging, but predictions in agricultural sciences are still tricky because agriculture is a highly complex system, with outcomes depending on a multitude of complex phenomena, such as weather, irrigation and soil properties. We propose future machine learning research in this sector to consider complex systems (chaos theory) and improve machine learning approaches.
In recent years machine learning has found its way into many areas of science, including physics, biology, finance, medicine, and agricultural sciences. Machine learning models are usually employed for analysis and predictions, such as stock price forecasts or population estimates. The more traditional approach of mechanistic models consists of mathematical machines with specific parameters set to perform well on a given task. Machine learning approaches, in contrast, are driven by historical data.
In agriculture, machine and deep learning have the potential to help forecast yields and nitrogen status [1]. For these tasks, it is necessary to use as many available sources of data as possible, e.g., remotely sensed data or historical yield and soil records. Here, as a rule of thumb, the broader the variety of data, the better. The reason for this is that agricultural production depends on many attributes, such as weather, soil properties, topography, irrigation, and fertiliser management. Results of these predictions are encouraging, but a lack of data and the complexity of the systems make predictions in agriculture difficult, i.e., the performance of the algorithms on test data in this sector thus far is insufficient for many applications.
On the other hand, the study of complex systems and chaos theory peaked in the 20th century. Many tools have been developed to measure the complexity of data and to estimate the chaotic behaviour of systems. Usually, those chaotic systems have many degrees of freedom and, therefore, strongly depend on the initial conditions under study. Since agricultural systems depend on many different attributes, we understand agricultural systems as complex systems (See cf. [2] for applications, such as chaotic plant population dynamics, spatio-temporal dynamics for arable land). Complexity can be found on various scales in agricultural systems, from the biological foundation of a single plant to the interactions between different crops, animals, and humans and the dependence on weather and climate interactions.
It is therefore important to consider the complex nature of the systems under study when doing analysis or predictions. Tools such as the Hurst exponent, the fractal dimension, entropy measures, or the spectrum of Lyapunov exponents may prove useful. These tools, which were developed to analyse chaotic or complex systems, are helpful to characterise and analyse agricultural systems. Methods such as the Hurst exponent are referred to as complexity measures, i.e., measuring the fluctuations or long-term memory of a system. Originally the Hurst exponent was invented for use in agriculture, specifically to determine the optimal dam sizes of the river of Nile to guarantee optimal irrigation of the surrounding land. The spectrum of Lyapunov exponents, in contrast, is a measure of the predictability of a system, and it can also estimate the degrees of freedom of a system.
To date, little research has combined the study of complex systems and machine and deep learning approaches, particularly within agricultural sciences. This may be because scientists working in agriculture rarely have expertise in this area of modelling, and likewise many computer scientists, although trained in mathematics, never hear about complex systems. There is usually primary education in physics and mathematics, but a course in complex systems is not part of the curriculum.
In [3], ideas from chaos theory and a neural network were used to predict geomagnetic activity. To be specific, a neural network approach has been improved using the Hölder exponent (Another complexity measure for time series related to the Hurst exponent). There are also some applications for finance where complexity measures have been used to improve predictions or estimate the volatility of data.
As an example of how to combine machine learning and chaos theory, the data stream of the proposed process is depicted in Figure 1. First, all available data sources are pre-processed using tools from chaos theory. In this step, irrelevant or too-noisy data is discarded, and a complexity value for each feature at every data point is calculated. This complexity value at each data point is referred to as a complexity feature. Second, only relevant data and the corresponding complexity features are fed into the machine learning algorithm to calculate yield predictions.
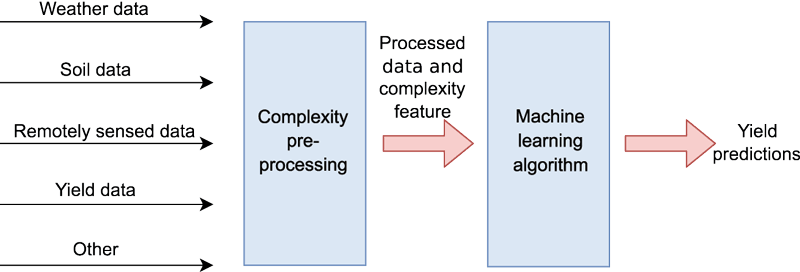
Figure 1: Schematic depiction of the proposed example. A multitude of data is fed into the preprocessing. The complexity-based preprocessing discards noisy data and adds a complexity feature to relevant data. A machine learning algorithm is then employed to predict yields.
We hope that the examples and references within this article serve to motivate researchers in both computer and agricultural sciences to learn about complex systems, chaos theory, and the corresponding tools. Because of its in-depth treatment of the system under study, a combination of machine learning and chaos theory may increase productivity and sustainability in agriculture.
The authors acknowledge the funding of the project “DiLaAg – Digitalization and Innovation Laboratory in Agricultural Sciences”, by the private foundation "Forum Morgen", the federal state of Lower Austria and by the FFG; Project AI4Cropr, No. 877158.
References:
[1] A. Chlingaryan, S. Sukkarieh, and B. Whelan: “Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review”, Computers and Electronics in Agriculture, 151:61–69, August 2018.
[2] K. Sakai: “Nonlinear Dynamics and Chaos in Agricultural Systems” ,Elsevier Science, Amsterdam, 1 edition, December 2001.
[3] Z. Vörös and D. Jankovičová: “Neural network prediction of geomagnetic activity: a method using local Hölder exponents”, Nonlinear Processes in Geophysics, 9(5/6):425–433, 2002.
Please contact:
Sebastian Raubitzek, Thomas Neubauer, Vienna University of Technology, Austria











