by Yous van Halder and Benjamin Sanderse (CWI)
Numerically solving the Navier-Stokes equations is an important tool in a wide range of industry applications involving fluid flow, but accurately solving them is computationally expensive. Many of these numerical solutions need to be computed, and a trade-off between computational time and accuracy needs to be made. At CWI we developed a method that attains a speed-up of up to 100 times when solving these equations, based on intrusive neural networks.
Recently developed machine-learning based fluid solvers can accurately simulate fluid flows significantly faster than conventional numerical approaches [L1, L2], but they are “non-intrusive”, i.e., the flow solver is used as a black-box [1,2]. This non-intrusiveness may result in unsatisfactory extrapolation of the machine learning algorithms outside the training set.
Our intrusive neural network approach uses a machine learning algorithm, a neural network, that is trained using both low- and high-fidelity data and is used intrusively in the solver which stimulates information transfer between the neural network and fluid solver to boost extrapolation capabilities. To be precise, we employ a convolutional/ deconvolutional neural network inside an existing numerical fluid solver, which is trained on a set of low- and corresponding high-fidelity solutions in a pre-processing stage. Convolutional layers in the neural network are used to extract non-observable latent quantities, while deconvolutional layers are used to effectively increase the dimensions of the input of the neural network. In our case the considered solver is a Particle In Cell/FLuid Implicit Particle (PIC/FLIP) [L3], which is a combination of a grid-based method, such as finite element, and particle-based method, such as smoothed particle hydrodynamics. The solver evolves a set of particles (representing the fluid) over time by computing fluid velocities on a Cartesian grid, where the fidelity of the simulation is determined by the resolution of the grid and the total number of particles. When a large number of particles is used, the accuracy is determined by the accuracy of the grid velocities, of which the accuracy is determined by the resolution of the grid. A parallel implementation of the PIC/FLIP solver can simulate millions of particles on a coarse grid in real-time and we therefore assume that the fidelity/computational cost is determined by the resolution of the grid. The idea is to run the PIC/FLIP fluid solver on a coarse grid, but to use a neural network inside the solver to enhance the effective resolution of the computational grid to accurately advect the particles. At first sight this might seem an impossible task, but enhancing coarse-grid solutions by using low-level features is in fact not new and is inspired by Large-Eddy Simulation (LES) for turbulence simulations, where the small turbulent scales are modelled using the quantities on the coarse grid.
We demonstrate how the multi-fidelity neural network approach works for simulating sloshing fluids. Sloshing fluids occur for instance when transporting a liquid that is contained in a ship carrier (see Figure 1). The ship’s motion induces a sloshing motion of the liquid in the transport tank, resulting in waves that impact the tank hull and may cause failure of the containment structure. A large set of numerical fluid simulations are required to assess the possible danger of liquid sloshing, given the enormous range of possible ship motions. The intrusive neural network approach enables each simulation to be performed at the cost of a low-fidelity simulation, while still obtaining accurate results.
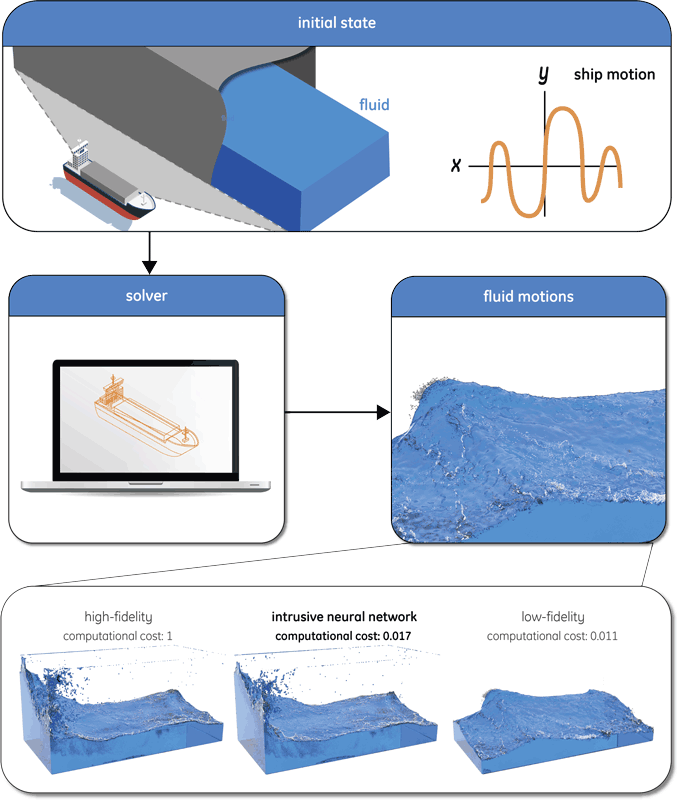
Figure 1: Intrusive neural networks can be used, for instance, to predict sloshing in a very effective and efficient way, making it possible to use it as a predictive tool for decision making. Our new method to solve Navier-Stokes equations for this and other applications in engineering is about 100 times faster than before, whilst maintaining almost the same accuracy.
Picture: CWI.
In this case, the deconvolutional neural network is trained on randomly generated low- and high-fidelity fluid sloshing data, which is obtained by creating an ensemble of simulations with random ship motions. This training data then consists of pairs of low- and high-fidelity solutions for which the neural network will serve as the mapping between the two fidelities. After training we can use our approach to enhance a low-fidelity sloshing simulation where the ship motion was different from the motions that were used during training. This gives a clear indication that our approach is indeed able to make predictions outside the training set. Example results are shown in Figure 1.
We clearly see a significant increase in accuracy with respect to the low-fidelity results, while the computational cost of our approach is approximately 100 times smaller than the high-fidelity computational cost. Our approach shows promising results when increasing the accuracy of a wide range of sloshing simulations. However, our approach is not yet able to enhance solutions that involve phenomena that were not encountered in the training set, e.g., obstacles in the flow. We expect that a carefully constructed training set may alleviate this issue.
Links:
[L1] https://github.com/byungsook/deep-fluids
[L2] https://www.youtube.com/watch?v=iOWamCtnwTc
[L3] https://blog.yiningkarlli.com/2014/01/flip-simulator.html
References:
[1] L. Ladický, et al.: “Data-driven fluid simulations using regression forests,” ACM Trans. Graph., vol. 34, no. 6, pp. 199:1–199:9, 2015.
[2] L. Ladický, et al.: “Physicsforests: real-time fluid simulation using machine learning,” in ACM SIGGRAPH 2017, pp. 22–22, 2017.
Please contact:
Yous van Halder
CWI, the Netherlands
Benjamin Sanderse
CWI, the Netherlands











