by Peter Rakyta (ELTE), Ágoston Kaposi, Zoltán Kolarovszki, Tamás Kozsik (ELTE), and Zoltán Zimborás (Wigner)
We are at the start of an exciting era for quantum computing, in which we are learning to manipulate many quantum degrees of freedom in a controlled way. At this point, it is vital for us to develop classical simulators of quantum computers to enable the study of new quantum protocols and algorithms. As the experiments move closer to realising quantum computers of sufficient complexity, their work must be guided by an understanding of what tasks we can hope to perform. Within the framework of the Quantum Information National Laboratory of Hungary [L1], we have developed a highly efficient photonic quantum computer simulator system, which is composed of Piquasso [L2], a flexible user-friendly general simulator of photonic quantum computers and of Piquasso Boost [L3], a high-performance simulator software stack. We report about this software system’s performance for simulating the Boson Sampling protocol focusing on Piquasso Boost and on its enhancement by a data-flow engine based permanent calculator device developed in a collaboration with Maxeler Technologies [L4].
Experimental setups successfully demonstrating boson-sampling (BS) provide an important milestone in the race to build universal quantum computers. Since BS experiments rely on multiphoton interference in linear optical interferometers, they do not have all the problem-solving ability of a universal quantum computer, but are suitable to solve some specific problems faster than today’s machines. There is currently a quest to find a set of practically important problems that could be mapped to this family of sampling schemes. This is partially motivated by the reasoning of Scott Aaronson showing the equivalence between searching and sampling problems [1].
The idea of BSBoson sSampling was introduced in the seminal work of Aaronson and Arkhipov [12]. They formulated the well-defined computational problem (sampling from the output distributions n indistinguishable photons that interfere during the evolution through an interferometer network), which could already provide a demonstration of a scalable quantum advantage over classical computers already with near-term photonic quantum devices. When scaling up the number of the photons passing through the interferometer at the same time, it becomes difficult to calculate the distribution of the output photons using conventional computers. The central mathematical problem to determine the probability of finding a given number of particles in the individual output modes of the interferometer is to evaluate the permanent function of the unitary matrix U describing the physics working behind the n-port interferometer:

where Sn labels the set of all permutations constructed from 1,2,...n. In fact, the permanent function is inherently encoded in the nature of the quantum world via fully symmetric wavefunctions used to describe indistinguishable bosonic particles. Thus, the ability to efficiently calculate the permanent is the key ingredient to simulate BS, which is crucial to explore possible applications of BS.
Currently the most efficient scalable approach to calculate the permanent of an n × n matrix A has a computational complexity of O(n2.2n), which can be further reduced to O(n.2n) if data recycling of intermediate results is implemented via Gray code ordering. The Ryser’s and the BB/FG formulas (named after Balasubramanian-Bax-Franklin-Glynn) follow quite different approaches to evaluate the permanent, also resulting in quite different numerical properties [3].
In our work we designed a novel scalable recursive implementation to calculate the permanent via the BB/FG formula following the idea of [4]. Our permanent algorithm has a computational complexity of O(n.2n) similarly to the Gray-code ordered algorithm of [3], without the overhead of processing the logic associated with the generation of auxiliary data needed for the Gray-code ordering. Instead, our algorithm relies on a recursive spawning of parallel tasks maximising the amount of computational data being recycled during the evaluation process. We compared the performance of our implementation provided in the Piquasso Boost library to the implementation of TheWalrus [L5] package also having implemented parallelised C++ engines to evaluate the permanent function. Our results (see Figure 1) show the logarithm of the average execution time needed to calculate the permanent of n×n random unitary matrices as the function of the matrix size n.
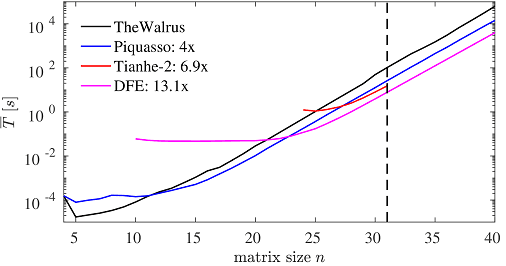
Figure 1: Benchmark comparison of individual implementations to calculate the permanent of an n x n unitary matrix. For better illustration, the discrete points corresponding to the individual matrices are connected by solid lines. The numbers associated with the individual implementations describe the speedup compared to the TheWalrus package at matrix size indicated by the vertical dashed line.
Our implementation is four times faster than TheWalrus code executed on 24 threads of Intel Xeon Gold 6130 CPU processor. We also compared the numerical performance of the Piquasso Boost simulation framework to the benchmark of Ref. [3]. In this case our benchmark comes very close to the execution time achieved on a single node of the Tianhe-2 supercomputer consisting of an Intel Xeon E5 processor with 48 threads and three Xeon Phi 31S1P cards with 684 threads in total. Our results indicate that the Piquasso package provides a high performance simulation framework even on smaller hardware. Our recursive implementation scales well on shared memory architectures, however, its scalability over distributed computational resources is limited [L6].
To efficiently perform permanent calculations on large scale computing resources we need to come up with an alternative approach. Here we report on a data-flow engine (DFE) based permanent calculator device. We developed a full-fledged permanent calculator implementation on Xilinx Alveo U250 FPGA cards using high-level data-flow programming tools developed by Maxeler Technologies. The data-flow engines are driven by the CPU of the host machines providing a high scalability of our implementation over MPI communication protocol: it is possible to divide the overall computational problem into chunks and distribute them over the nodes of a supercomputer cluster just like in the case of the CPU implementation of [3].
Our FPGA-based DFEs have several advantages over CPU and GPU technologies. Probably the most important aspect of FPGA is the possibility to have hardware support for arithmetic operations exceeding the precision of 64-bit arithmetic units of CPU and GPU hardware. In practical situations the permanents of unitary matrices describing the photonic interferometers would be much smaller than the individual elements of the input matrix. In this situation one needs to increase the numerical precision in the calculations to obtain a result that can be trusted. In fact, the implementations of the walrus package and the Piquasso Boost library already use extended precision for floating point operations on the CPU side to calculate the permanent. On the DFE side we used 128-bit fixed point number representation to perform the calculations, providing the most accurate result among the benchmarked implementations.
Figure 1 also shows the performance of our DFE permanent calculator compared to the previously discussed CPU implementations. We observe that on DFE we can calculate the permanents of larger matrices much faster than by CPU based implementations with a numerical precision exceeding them. Note that at smaller matrices the execution time is dominated by the data transfer through the PCI slot.
In our future work we aim to use our highly optimized Piquasso simulations framework to address computational problems related to BS and examine the possibility of using BS quantum devices to solve real world computational problems. Our efficient method to evaluate the permanent would be valuable in other research works as well, making the evaluation of the amplitudes of many-body bosonic states faster and more reliable.
This project has received funding from the Ministry of Innovation and Technology and the National Research, Development and Innovation Office within the Quantum Information National Laboratory of Hungary.
Links:
[L1] https://qi.nemzetilabor.hu/
[L2] https://github.com/Budapest-Quantum-Computing-Group/piquasso
[L3] https://github.com/Budapest-Quantum-Computing-Group/piquassoboost
[L4] https://www.maxeler.com/
[L5] https://github.com/XanaduAI/thewalrus
[L6] https://arxiv.org/abs/2109.04528
References:
[1] S. Aaronson, A. Arkhipov: “The computational complexity of linear optics”, in Proc. of STOC’11 https://dl.acm.org/doi/10.1145/1993636.1993682
[2] J. Wu, et al.: “A benchmark test of boson sampling on Tianhe-2 supercomputer”, National Science Review, Volume 5, Issue 5, September 2018, Pages 715–720, https://doi.org/10.1093/nsr/nwy079
Please contact:
Peter Rakyta
Eötvös Loránd University, Hungary











