by Ioannis G. Karafyllidis (Democritus University of Thrace)
The quantum walk model of quantum computation can be used to conceive and develop new quantum algorithms for real-life practical applications.
The dominant quantum computation model is the quantum circuit or quantum gate model, in which quantum algorithms are expressed as quantum circuits, but is difficult to conceive new quantum algorithms for real-life practical applications using this model. Quantum walks is a universal quantum computation model and its concept can be directly applied for solving practical problems and studying many physical systems and processes.
Quantum walks represent quantum evolution in continuous spaces, discrete lattices and graphs. In this model, the motion of a quantum walker is guided by the action of unitary operators derived from Hamiltonians that describe the specific problem at hand. Quantum walks have been proven to be a universal model for quantum computation. Continuous quantum walks on graphs can encode any quantum computation with quantum gates implemented by scattering processes [1]. Discrete quantum walks have been proven to implement the same universal quantum gate set and thus are able to implement any quantum algorithm [2]. Quantum walks can also be encoded as quantum circuits, which is also a universal model for quantum computation. Furthermore, quantum walks on the graphene lattice with quantum gates as coins may prove to be an effective implementation of quantum computing [3].
In the Department of Electrical and Computer Engineering of the Democritus University of Thrace, Greece, we used quantum walks to develop quantum algorithms as a part of a hybrid classical/quantum computing system for autonomous driving and traffic control. In this approach each vehicle is modelled as a quantum walker moving in an urban area. Potential barriers are introduced to represent moving obstacles, such as other vehicles, immovable obstacles, such as sidewalks and buildings, and time-varying obstacles, such as traffic lights.
Figure 1(a) shows a vehicle accelerating to the right. The acceleration is introduced as a linear potential (red line) and the blue bars indicate the probability of the vehicle’s location in the near future. Figure 1 (b) shows a vehicle decelerating in the presence of a red traffic light introduced as a potential barrier. Traffic lights are modelled as time-varying potential barriers. Red light corresponds to a high potential barrier with near-zero transmission coefficient and green light to no potential barrier. Yellow light corresponds to a potential barrier with varying height. The moment the yellow light is on, the height of the potential barrier is zero and increases with time until its height becomes equal to the red light barrier height, the moment at which the yellow light goes off and the red is on.
Probable collisions between vehicles can be detected prior to their occurrence from the interference between the probability amplitudes associated with each moving vehicle, modeled as a quantum walker. Figure 2 shows such a case. Two vehicles moving in opposite directions with different velocities disperse a probability amplitude “cloud” in front of them and the interference indicates the probability and location of the collision.
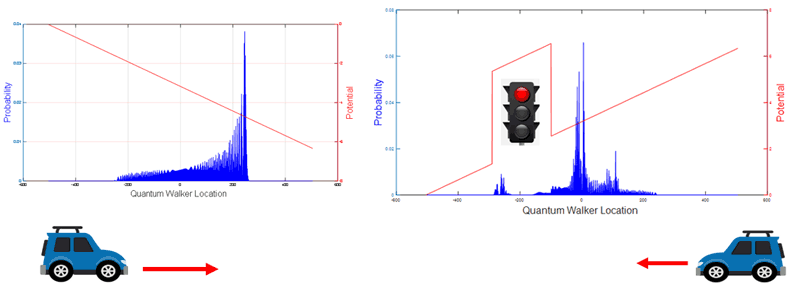
Figure 1: (a) vehicle accelerating to the right. (b) A vehicle decelerating in the presence of a red traffic light modelled as a potential barrier.

Figure 2: Probability and location of possible collision between two vehicles (interference between two quantum walkers).
Figure 3 shows how urban areas are introduced using potential barriers. Immovable objects such as sidewalks and buildings are represented by constant potential barriers with near-zero transmission coefficients. Traffic lights are represented by time-varying potential barriers as explained above. Vehicles, i.e., quantum walkers move in this potential space.
Future work includes vehicle routing in urban areas. In this case, the driver enters their current location and destination in a GPS navigation system, which, via 5G networks, communicates the information to the control centre. A quantum computer may hold in superposition many vehicle positions and destinations and optimise traffic flow by proposing a route to each driver.
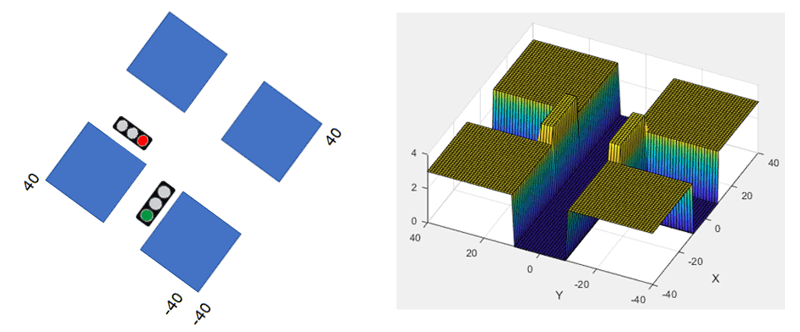
Figure 3: Urban areas are modeled by constant potential barriers (sidewalks and buildings) and time-varying potential barriers (traffic lights).
References:
[1] A. M. Childs: “Universal computation by quantum walk”, Physical Review Letters 102, 180501 (2009).
[2] N. B. Lovett, et al.: “Universal quantum computation using the discrete-time quantum walk”, Physical Review Letters 81, 042330 (2010).
[3] I. G. Karafyllidis: “Quantum Walks on Graphene Nanoribbons using Quantum Gates as Coins”, Journal of Computational Science, vol. 11, pp. 326-330, 2015.
Please contact:
Ioannis G. Karafyllidis
Democritus University of Thrace, Greece
+30 25410 79548











