by Maxime Garnier and Harold Ollivier (Inria)
Delegation, privacy and integrity of quantum computations are prerequisites for quantum computing to have a real-world economic impact. Companies will not buy machines but rather access services on demand through service providers. In doing so, they need to be confident that the computations are executed correctly while not putting their data and intellectual property at risk. The recently introduced protocol of [1] is the first practical solution towards achieving this goal as it provides security through disentangled single qubit quantum communications without hardware overhead on the provider's side while also being robust to noise. As a result, it is considered a blueprint use case for quantum networks and can provide design guidelines for security for quantum computers.
Remotely accessible quantum computing platforms alleviate the burden of maintaining complex physical devices in house. Yet, when delegating computations to quantum servers, clients want guarantees on the privacy of their data and algorithms, and on the faithfulness of the computations’ executions.
Existing protocols to achieve this can be assigned to two broad categories: those that do not require quantum capabilities on the client side, and those that require modest ones. While at first sight the former [2] seems the most appealing option, it requires so much overhead on the server side that it will remain out of reach for several decades – the over-head is estimated to be several hundred times. The latter (e.g. [3]) is indeed more realistic. In this setting, computations are performed using the measurement-based quantum computation (MBQC) model, which is particularly well-suited for delegated, blind and verifiable computations. There, the client only needs to perform single qubit transformations and to send these qubits to the server in order to get all three properties.
Nonetheless, before [1], prospects for practical protocols were grim. First, all existing options were overly sensitive to noise, turning insecure noisy machines into secure but use-less ones. Indeed, these protocols were designed to detect any deviation and abort quickly, hence mistaking plain hardware noise for a malicious behaviour. Second, they verify that computations are performed according to the instructions sent by the client by blindly inserting traps – small computations with known results. These are then checked to determine whether to accept or abort. Unfortunately, these traps have finite detection capability and their sensitivity needs to be boosted by a layer of fault-tolerant encoding to allow for the detection of malicious behaviour with overwhelming probability. Because of the large overhead imposed by such encoding, clients with a fixed number of good qubits need to decide whether to devote them to computing or securing the computations themselves.
In [1], the necessity for this trade-off was removed because the authors found that trap sensitivity could be boosted much more efficiently for bounded quantum polynomial (BQP) time computations – i.e. the kind of computations that quantum computers can perform efficiently. First, instead of inserting traps alongside the computation itself, they are inserted on specific rounds – called test rounds – that share the same underlying structure as the computation itself. Second, because BQP computations have classical input and out-put, computation rounds and test rounds can be repeated before a final decision is made using majority voting. Together with blindness, this makes it possible to boost trap sensitivity and protect computation from noise. This is because repetition and majority vote act as an error correction scheme and protect computation from noise. Yet at the same time, the malicious server needs to deviate beyond the error correction capabilities of the scheme to have an effect on the computation, hence making its deviations easier to detect. Together, these two properties ensure that verification and blindness can be achieved without hardware overhead, except repetition, since the computation and test rounds have the same structure and thus the same requirements. In addition, the security of the protocol is achieved in the demanding composable framework of abstract cryptography ensuring the validity of the results even when the protocol is used as part of a bigger protocol, or repeated several times in parallel or in series.
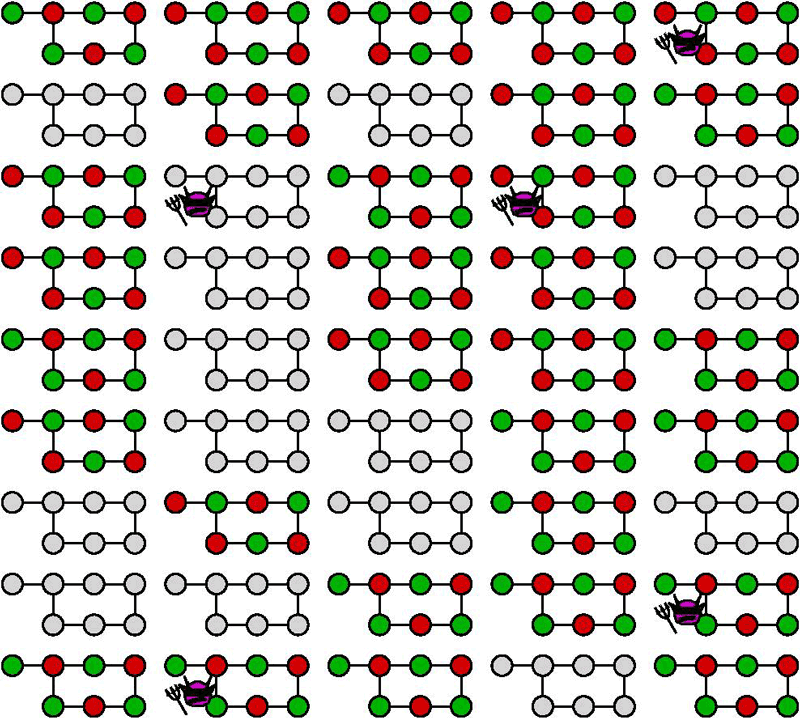
Figure 1: Each connected graph represents a given measurement-based pattern that is executed by the server, where each node in the graph represents a qubit. When a grey pattern is executed, it corresponds to the computation delegated by the client, while green and red ones represent delegated test rounds. Because the delegation is executed blindly, the malicious server (purple demon) does not know where to attack the computation, it inevitably gets detected by some test rounds. The advantage of the scheme is to ensure that each executed pattern has the same requirement as the computation itself while giving cryptographic guarantees with exponentially low correctness and soundness errors at the expense of a polynomial number of delegated rounds. Each connected graph represents a given measurement-based pattern that is executed by the server, where each node in the graph represents a qubit. When a grey pattern is executed, it corresponds to the computation delegated by the client, while green and red ones represent delegated test rounds. Because the delegation is executed blindly, the malicious server (purple demon) does not know where to attack the computation, it inevitably gets detected by some test rounds. The advantage of the scheme is to ensure that each executed pattern has the same requirement as the computation itself while giving cryptographic guarantees with exponentially low correctness and soundness errors at the expense of a polynomial number of delegated rounds.
Thanks to these properties – and a few more technical ones – this protocol is considered a potential blueprint for quantum network applications within the Quantum Internet Alli-ance project of the Quantum Flagship. Yet, its interest goes beyond that of an experimental realisation.
First, it is economically relevant for the development of quantum computing. As noted earlier, quantum computers will only be accessible through the cloud. The current situation where data and algorithms are shared with the service providers is acceptable only because companies are still learning about quantum algorithms and trying to discover applications. This will change drastically when production applications develop to the point where the security of quantum computations will be a prerequisite. Hence, the described protocol is clearing the path for real-world use of quantum computers.
Second, it uncovered new techniques for trap design and insertion that can find broader applications. One of them, currently being investigated, allows the service provider to recover a noise map that would be useful to reduce downtime for recalibration of its machines.
Third, the overhead for secure multi-party BQP computations can likely be drastically reduced using similar techniques. This would allow several clients to collectively obtain the result of a global computation without putting the privacy of their data at risk – typical use cases include AI model training for financial institutions or healthcare where manipulated data is highly regulated.
Finally, because it shows that security does not reduce the ability to perform complex quantum computations, there is no reason to not include security as a requirement for the design of future quantum hardware. This means that quantum computers should be able to receive quantum states as inputs from the clients, and that quantum networks should be developed to match these needs.
References:
[1] D. Leichtle et al.: “Verifying BQP Computations on Noisy Devices with Minimal Over-head”, PRX Quantum 2, 040302, 2021. DOI:10.1103/PRXQuantum.2.040302
[2] U. Mahadev: “Classical Verification of Quantum Computations”, 59th IEEE Annual Symposium on Foundations of Computer Science (FOCS) 2018, Paris, pp 259-267.
[3] E. Kashefi and P Wallden: “Optimised resource construction for verifiable quantum computation”, Journal of Physics A: Mathematical and Theoretical, 50, 145306, 2017.
Please contact:
Harold Ollivier, Inria, France











