by Caroline Lawitschka and Sebastian Schrittwieser (University of Vienna)
We introduce a novel methodology for generating complex and robust Mixed Boolean-Arithmetic (MBA) expressions for various software protection methodologies. Our research specifically focuses on leveraging the concept of equality saturation to create MBA expressions of arbitrary complexity.
Mixed Boolean-Arithmetic (MBA) expressions combine Boolean logic operations such as AND, OR, XOR, and NOT with arithmetic operations like addition (+), subtraction (-), multiplication (*), and division (/). This combination provides a powerful tool for creating complex expressions that can be used in code obfuscation.
Code obfuscation is a broad term encompassing techniques used to make program code more difficult to understand, analyse, and reverse-engineer, thereby protecting intellectual property and preventing software tampering. In the software protection domain, MBA expressions are often used to generate opaque predicates, which always evaluate to either true or false, independently from their inputs. While the software developer knows the evaluation result of the opaque predicate, it is time-consuming for an attacker to figure out its input-independence and the correct evaluation result. In practice, opaque predicates help create fake branches with paths that are never executed at runtime. The effectiveness of MBA in obfuscation techniques has been well-documented in the literature. For instance, Zhou et al. [1] demonstrated how MBA expressions can be utilised for information hiding in software, highlighting the robustness of MBA-based obfuscation methods against various analysis techniques.
However, MBA-based obfuscations are not invincible. Recent years have seen significant efforts to develop methods for breaking and simplifying MBA expressions. These efforts are driven by the need to analyse and understand obfuscated code, whether for debugging purposes, reverse engineering, or detecting malicious software. As obfuscation methods become more sophisticated, so do the techniques for breaking them.
In our research at the Christian Doppler Laboratory for Assurance and Transparency in Software Protection [L1], we focus on a novel methodology for generating strong and verifiable MBA expressions based on the concept of equality saturation. In particular, we build e-graphs for the generation of arbitrarily complex MBA expressions.
In 2009, Tate et al. [2] proposed equality saturation as a new optimisation technique which is based on the e-graph data structure. An e-graph is a graph structure that represents a congruence relation over a set of expressions. It consists of equivalence classes (e-classes), each containing equivalent nodes (e-nodes). E-nodes are unique, and the children of e-nodes are references to e-classes. Term rewriting involves transforming a term based on a set of possible rewriting rules without losing its semantics. E-graphs can efficiently express these equivalent terms.
Equality saturation is a technique for program optimisation based on the e-graph structure. Simply put, equality saturation explores all expressions possible within the existing rewrite rules and then selects the best one (e.g. fastest) for a specific use case based on a cost function. The advantage over iterative term rewriting is that equality saturation can find global optima.
The fundamental idea behind our novel approach is to construct strong opaque predicates – expressions that always evaluate to true or false but are difficult to analyse – from simple MBA expressions. Using equality saturation, these simple expressions are transformed into more complex ones that are semantically equivalent but much harder to understand and analyse. This transformation is guided by an e-graph structure, where rewriting rules are applied iteratively to generate increasingly complex expressions. While e-graphs and equality saturation have previously been used for deobfuscation of MBA expressions, we revere this process and generate arbitrarily complex expressions from simple ones.
Our research involved creating a comprehensive set of rewriting rules that describe equivalent expressions, ranging from basic arithmetic properties to more complex transformations. For example, a simple rewriting rule might describe the commutative property of multiplication, where the expression (a * b) can be rewritten as (b * a). A more complex rule could involve the transformation of an expression involving bitwise negation, such as rewriting ~(a + b) as (~a + ~b + 1). These rewriting rules were manually and systematically generated to cover a wide range of possible transformations, ensuring that the resulting MBA expressions are both complex and semantically equivalent to the original expressions.
To create arbitrarily complex MBA expressions starting from a randomly chosen simple expression, an increasingly complex e-graph is generated iteratively by applying these rewriting rules. Figure 1 illustrates the concept using a trivial example. Our starting point for the construction of a complex MBA expression is the term (a & b) | b. The only rewriting rule applied to the e-graph is the commutative rule (a & b) = (b & a). Iteratively, many more rewriting rules are applied until a complex e-graph containing all possible equivalences emerges. Each iteration of this process results in a more complex expression, ultimately leading to an MBA expression that is highly resistant to analysis.
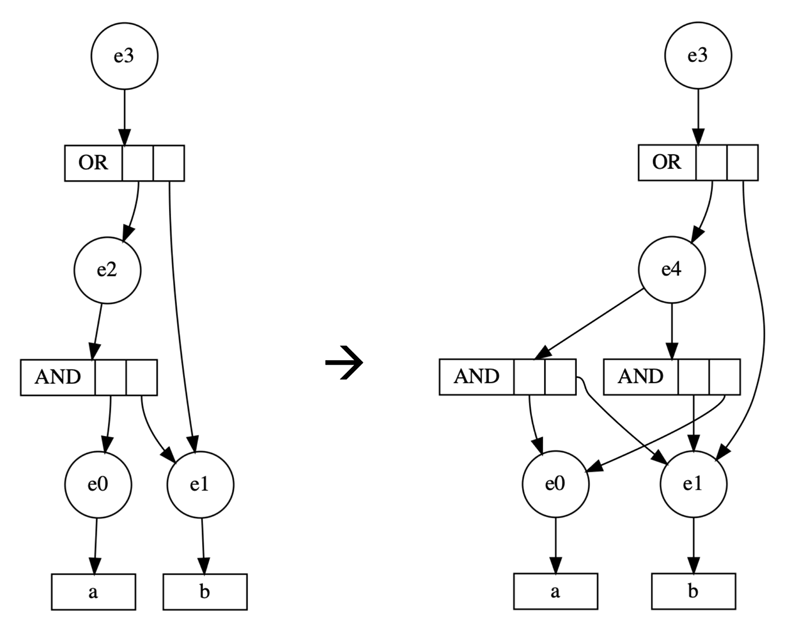
Figure 1: Building an e-graph with one simple rewriting rule.
In conclusion, our research introduces a novel methodology for generating complex and verifiable MBA expressions by leveraging the concepts of e-graphs and equality saturation, providing a robust solution for generating arbitrarily complex opaque predicates used for software protection.
Link:
[L1] https://cdl-astra.at
References:
[1] Y. Zhou, et al. “ Information hiding in software with mixed boolean-arithmetic transforms,” in Int. Workshop on Information Security Applications, pp. 61–75, Springer, 2007.
[2] R. Tate, et al. “Equality saturation: a new approach to optimization”, in Proc. of the 36th annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pp. 264–276), 2009.
Please contact:
Caroline Lawitschka, Christian Doppler Laboratory for Assurance and Transparency in Software Protection, Faculty of Computer Science, University of Vienna, Austria
caroline.lawitschka @univie.ac.at











