by Chenglu Jin (CWI) and Marten van Dijk (CWI and Vrije Universiteit)
For a long time, process variations in the manufacturing of computer chips has been a big hurdle for producing high-quality products. However, one can turn these imperfections caused by the process variations into something good: into unique random functions that are impossible to clone even by the original manufacturer. At CWI in Amsterdam, we are building a solid foundational understanding of these security primitives and bringing them closer to practice. This could be very interesting for use in computer systems and embedded systems, like cloud servers and controllers in critical infrastructures.
A Physical Unclonable Function (PUF) is a hardware security primitive, and its input-output behaviour (also called Challenge-Response Pairs or CRPs) depends on the uncontrollable and unclonable manufacturing process variation introduced in the manufacturing process of a semiconductor chip [1]. Hence, even the same manufacturer cannot physically clone a fabricated PUF device with the same behaviour.
One classical PUF design is Arbiter PUF (originally introduced by Marten van Dijk and his collaborators), as shown in Figure 1. It consists of a chain of switch components and ends with an arbiter. Each switch component propagates the two inputs on the left to the two outputs on the right via either the crossed paths or the parallel paths, depending on the value of the top selection bit input. Since the delay difference between the selected pair of paths is designed to be as small as possible, the main factor that will affect the delay difference is the manufacturing process variations. To evaluate an Arbiter PUF, the user first provides challenge bits to the selection bits of the switch chain and then sends a pulse signal from the left end of the switch chain. Every challenge-response pair should only depend on the process variation in the delay difference selected by the challenge bits.
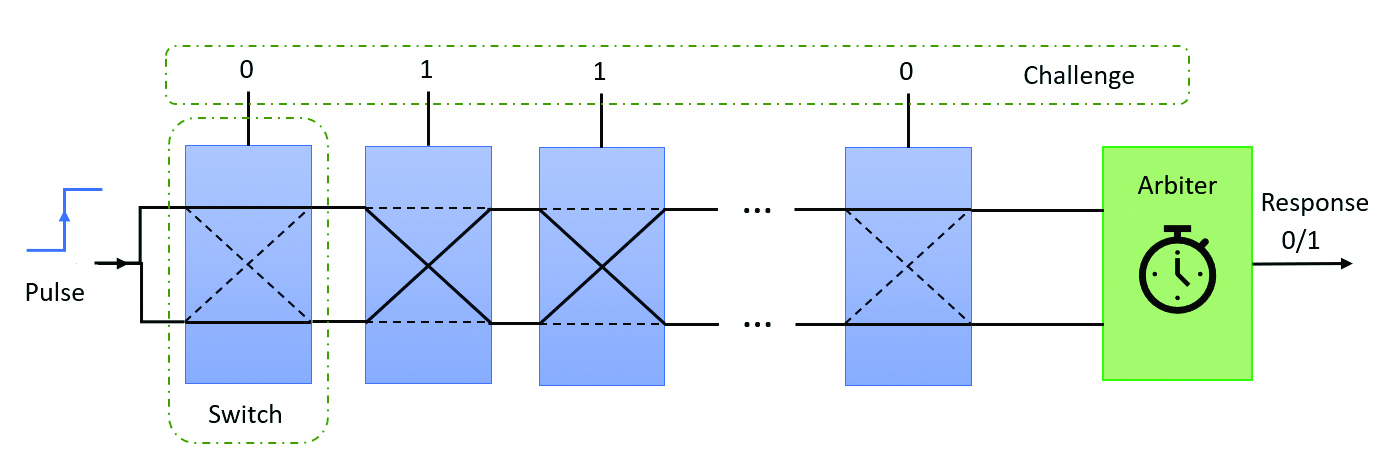
Figure 1: The basic operation of an Arbiter Physical Unclonable Function. Physical properties of chips like these are unique. Their uniqueness can be used to add security to critical infrastructure systems.
This unclonable feature allows PUF to enable many security applications. The most traditional use case of PUF is device authentication. Since there are no two PUFs in the world that have the exact same input-output behaviour, a verifier is able to remotely check whether the counterparty holds the PUF by checking whether the prover can send the responses to a few random challenges chosen by the verifier. The verifier just needs to compare the responses from the prover with the responses stored in its CRP database collected when it holds the PUF. If the prover does not hold the PUF at the moment, the prover will not be able to generate the correct responses, even if it had access to the PUF before. This is because the possible challenge space of the PUF is extremely large; without knowing which challenges will be selected by the verifier beforehand, the probability of the dishonest prover successfully predicting the used challenges would be extremely low. Thus, PUF provides a very lightweight and reliable method to perform device authentication in practice. Moreover, PUFs can be used to construct secure cryptographic protocols, like key agreement, oblivious transfer, and bit commitment.
PUF is also very useful in providing architectural support for software security. For example, PUF can be used for key management and remote attestation. PUF-based key management has a unique advantage over traditional key management, which stores secret keys in a digital memory. A digital memory may be vulnerable to probing attacks. A PUF-based key management scheme uses the responses of a PUF as the secret keys, while only the corresponding challenges need to be stored in a digital memory, which can be public information known by attackers. The secret keys will only be revealed during the runtime after the PUF has been fed with the stored challenges. Additionally, one can further extend this idea to construct secure remote attestation protocols, where a verifier will be able to check whether the outsourced code and data are executed on the authenticated processor embedded with a genuine PUF.
All of the above use cases have demonstrated the promising potential of the PUF technology, and the security of these protocols can be reduced to the security of the PUF itself. However, attackers could also build a mathematical clone of a PUF that can predict all of its CRPs. Even with some of the state-of-the-art PUF designs, advanced modelling attacks can still achieve substantially better accuracy (e.g. 75%) than random guesses (50%). So, until now, this type of attack has significantly undermined the security of the PUF and any security protocols or mechanisms built on it.
To solve this problem, we would want PUFs to have the same behaviour as a physical random oracle. A random oracle is supposed to generate an independent random value output from a uniform distribution when given a new and unseen input, and if it receives an input that has been queried before, it should reply with the same output as last time. However, PUF evaluations are sensitive not only to the process variations but also to measurement noise. Thus, sometimes, even the same challenge will lead to different responses on the same PUF. To overcome the reliability issue, one needs to post-process raw PUF responses before revealing them to the adversary. One popular post-processing method is called fuzzy extractor, and it is designed to extract a reliable secret string from a fuzzy input, which is the raw PUF responses [2]. However, to keep the security of the whole system, the computation inside the fuzzy extractor has to be kept secret from the adversary.
In our recent work, we introduce a theoretical framework that does not require any confidential digital computing while we can still prove rigorous statements about the bit security of a system that interfaces with the PUF [3]. The framework is even secure when the adversary has a prediction model (e.g. with a 75% accuracy). In particular, we proved the bit security of a PUF-based random oracle construction. This merges the PUF framework with fuzzy extractors. This gives hope for us to rigorously analyse the security of all the systems and protocols built on top of PUF.
Link:
[L1]: https://www.cwi.nl/en/groups/computer-security/
References:
[1] B. Gassend, et al. “Silicon physical random functions,” in Proc. of the 9th ACM Conference on Computer and Communications Security, 2002.
[2] Y. Dodis, L. Reyzin, and A. Smith, “Fuzzy extractors: How to generate strong keys from biometrics and other noisy data,” Advances in Cryptology-EUROCRYPT 2004: Int. Conf. on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004. Proceedings 23, Springer, 2004.
[3] M. van Dijk and C. Jin. “A theoretical framework for the analysis of physical unclonable function interfaces and its relation to the random oracle model,” J. of Cryptology, 36.4 (2023): 35.
Please contact:
Chenglu Jin, CWI, the Netherlands
Marten van Dijk, CWI, the Netherlands











