by Bojian Yin (CWI), Federico Corradi (IMEC Holst Centre) and Sander Bohté (CWI)
Although inspired by biological brains, the neural networks that are the foundation of modern artificial intelligence (AI) use exponentially more energy than their counterparts in nature, and many local “edge” applications are energy constrained. New learning frameworks and more detailed, spiking neural models can be used to train high-performance spiking neural networks (SNNs) for significant and complex tasks, like speech recognition and EGC-analysis, where the spiking neurons communicate only sparingly. Theoretically, these networks outperform the energy efficiency of comparable classical artificial neural networks by two or three orders of magnitude.
Modern deep neural networks have only vague similarities with the functioning of biological neurons in animals. As illustrated in Figure 1 (left), many details of biological neurons are abstracted in this model of neural computation, such as the spatial extent of real neurons, the variable nature and effect of real connections formed by synapses, and the means of communication: real neurons communicate not with analogue values, but with isomorphic pulses, or spikes, and they do so only sparingly.
As far back as 1997, Maass argued that mathematically, networks of spiking neurons could be constructed that would be at least as powerful as similar sized networks of standard analogue artificial neurons [1]. Additionally, the sparse nature of spike-based communication is likely key to the energy-efficiency of biological neuronal networks, an increasingly desirable property as artificial intelligence (AI) energy consumption is rapidly escalating and many edge-AI applications are energy-constrained. Until recently, however, the accuracy of spiking neural networks (SNNs) was poor compared to the performance of modern deep neural networks.
A principal obstacle for designing effective learning rules in SNNs has always been the discontinuous nature of the spiking mechanism: the workhorse of deep learning is error-backpropagation, which requires the estimation of the local gradient between cause and effect. For spiking neurons, this requires, for example, estimating how changing an input weight into a neuron affects the emission of spikes. This, however, is discontinuous: the spiking mechanism is triggered when the input into the neuron exceeds an internal threshold, and a small change in weight may be enough to just trigger a spike or prevent a spike from being emitted. To overcome the problem of learning with such discontinuous gradients, recent work [2] demonstrated a generic approach by using a “surrogate gradient”. Importantly, the surrogate gradient approach enables the use of modern deep learning software frameworks like PyTorch and Tensorflow, including their efficient optimisers and GPU-support.
In joint work from CWI and IMEC [3], we demonstrate how surrogate gradients can be combined with efficient spiking neuron models in recurrent spiking neural networks (SRNNs) to train these networks to solve hard benchmarks using Back-Propagation-Through-Time: the SRNN is illustrated in Figure 1 (right). In particular, we showed how an adaptive version of the classical “leaky-integrate-and-fire” spiking neuron, the Adaptive LIF (ALIF) neuron, enables the networks to achieve high performance by co-training the internal parameters of the spiking neuron model that determine its temporal dynamics (the membrane-potential time-constant and the adaptation time-constant) together with the weights in the networks.
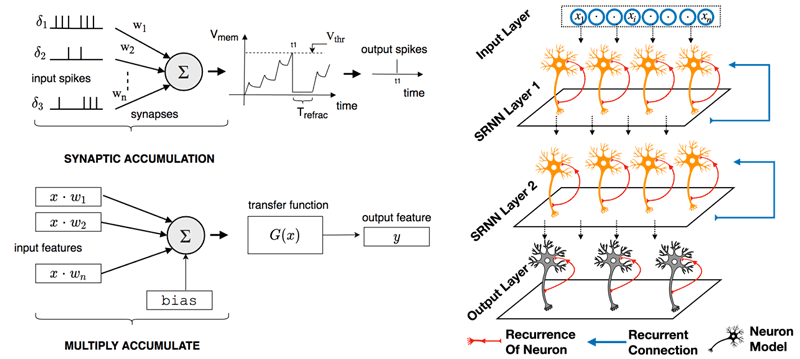
Figure 1: Left: operation of spiking neurons compared to analogue neural units. Neurons communicate with spikes. Each input spike adds a weighted (and decaying) contribution to the internal state of the targeted neuron. When this state exceeds some threshold from below, a spike is emitted, and the internal state is reset. In the analogue neural unit, inputs x are weighted with corresponding weights w to add to the neuron’s internal state, from which the neuron’s output G(x) is computed. Right: illustration of a spiking recurrent neural network. Red connections denote the effective self-recurrence of spiking neurons due to the dynamic internal state.
With these adaptive SRNNs, we achieve new state-of-the-art performance for SNNs on several tasks of inherent temporal nature, like ECG analysis and speech recognition (SHD), all while demonstrating highly sparse communication. Their performance also compared favourably to standard recurrent neural networks like LSTMs and approaches the current state of the art in deep learning. When comparing computational cost as a proxy for energy consumption, we calculated the required Multiply-Accumulate (MAC) and Accumulate (AC) operations for various networks. With a MAC being about 31x more energetically expensive compared to an AC, and with spiking neurons using ACs sparingly where MACs are used in standard neural networks, we demonstrate theoretical energy advantages for the SRNNs ranging from 30 to 150 for comparable accuracy (for more details, see [3]).
We believe this work demonstrates that SNNs can be compelling propositions for many edge-AI applications in the form of neuromorphic computing. At the same time, tunable spiking neuron parameters proved essential for achieving such accuracy, suggesting both novel venues for improving SNNs further and neuroscientific investigations into corresponding biological plasticity.
Links:
Project: NWO TTW programme “Efficient Deep Learning”, Project 7, https://efficientdeeplearning.nl/
Pre-print: https://arxiv.org/abs/2005.11633
Code: https://github.com/byin-cwi/SRNN-ICONs2020
References:
[1] W. Maass: “Fast sigmoidal networks via spiking neurons. Neural Computation”, 9(2), 279-304, 1997.
[2] E.O.Neftci, H. Mostafa, F. Zenke: “Surrogate gradient learning in spiking neural networks: Bringing the power of gradient-based optimization to spiking neural networks”, IEEE Signal Processing Magazine, 36(6), 51-63, 2019.
[3] B. Yin, F. Corradi, S.M. Bohté: “Effective and efficient computation with multiple-timescale spiking recurrent neural networks”, in Int. Conf. on Neuromorphic Systems 2020 (pp. 1-8), 2020; Arxiv 2005.11633v1
Please contact:
Sander Bohte, CWI, The Netherlands











