by Timothée Masquelier (UMR5549 CNRS – Université Toulouse 3)
Back-propagation is THE learning algorithm behind the deep learning revolution. Until recently, it was not possible to use it in spiking neural networks (SNN), due to non-differentiability issues. But these issues can now be circumvented, signalling a new era for SNNs.
Biological neurons use short electrical impulses called “spikes” to transmit information. The spike times, in addition to the spike rates, are known to play an important role in how neurons process information. Spiking neural networks (SNNs) are thus more biologically realistic than the artificial neural networks (ANNs) used in deep learning, and are arguably the most viable option if one wants to understand how the brain computes at the neuronal description level. But SNNs are also appealing for AI, especially for edge computing, since they are far less energy hungry than ANNs. Yet until recently, training SNNs with back-propagation (BP) was not possible, and this has been a major impediment to the use of SNNs.
Back-propagation (BP) is the main supervised learning algorithm in ANNs. Supervised learning works with examples for which the ground truth, or “label”, is known, which defines the desired output of the network. The error, i.e., the distance between the actual and desired outputs, can be computed on these labelled examples. Gradient descent is used to find the parameters of the networks (e.g., the synaptic weights) that minimise this error. The strength of BP is to be able to compute the gradient of the error with respect to all the parameters in the intermediate “hidden” layers of the network, whereas the error is only measured in the output layer. This is done using a recurrent equation, which allows computation of the gradients in layer l-1 as a function of the gradients in layer l. The gradients in the output layer are straightforward to compute (since the error is measured there), and then the computation goes backward, until all gradients are known. BP thus solves the “credit assignment problem”, i.e., it finds the optimal thing to do for the hidden layers. Since the number of layers is arbitrary, BP can work in very deep networks, which has led to the widely talked about deep learning revolution.
This has motivated us and others to train SNNs with BP. But unfortunately, it is not straightforward. To compute the gradients, BP requires differentiable activation functions, whereas spikes are “all-or-none” events, which cause discontinuities. Here we present two recent methods to circumvent this problem.
S4NN: a latency-based backpropagation for static stimuli.
The first method, S4NN, deals with static stimuli and rank-order-coding [1]. With this sort of coding, neurons can fire at most one spike: most activated neurons first, while less activated neurons fire later, or not at all. In particular, in the readout layer, the first neuron to fire determines the class of the stimulus. Each neuron has a single latency, and we demonstrated that the gradient of the loss with respect to this latency can be approximated, which allows estimation of the gradients of the loss with respect to all the weights, in a backward manner, akin to traditional BP. This approach reaches a good accuracy, although below the state-of-the-art: e.g., a test accuracy of 97.4% for the MNIST dataset. However, the neuron model we use, non-leaky integrate-and-fire, is simpler and more hardware friendly than the one used in all previous similar proposals.
Surrogate Gradient Learning: a general approach
One of the main limitations of S4NN is the at-most-one-spike-per-neuron constraint. This constraint is acceptable for static stimuli (e.g., images), but not for those that are dynamic (e.g., videos, sounds): changes need to be encoded by additional spikes. Can BP still be used in this context? Yes, if the “surrogate gradient learning” (SGL) approach is used [2].
The most commonly used spiking neuron model, the leaky integrate-and-fire neuron, obeys a differential equation, which can be approximated using discrete time steps, leading to a recurrent relation for the potential. This relation can be computed using the recurrent neural network (RNN) formalism, and the training can be done using back-propagation through time, the reference algorithm for training RNNs. The firing threshold causes optimisation issues, but they can be overcome by using a “surrogate gradient”. In short, in the forward pass of BP, the firing threshold is applied normally, using the Heaviside step function. But in the backward pass, we pretend that a sigmoid was used in the forward pass instead of the Heaviside function, and we use the derivative of this sigmoid for the gradient computation. This approximation works very well in practice. In addition, the training can be done using automatic-differentiation tools such as PyTorch or Tensorflow, which is very convenient.
We extended previous approaches by adding convolutional layers (see [3] for a similar approach). Convolutions can be done in space, time (which simulates conduction delays), or both. We validated our approach on a speech classification benchmark: the Google speech commands dataset. We managed to reach nearly state-of-the-art accuracy (94.5%) while maintaining low firing rates (about 5Hz, see Figure 1). Our study has just been accepted at the IEEE Spoken Language Technology Workshop [4]. Our code is based on PyTorch and is available in open source at [L1].
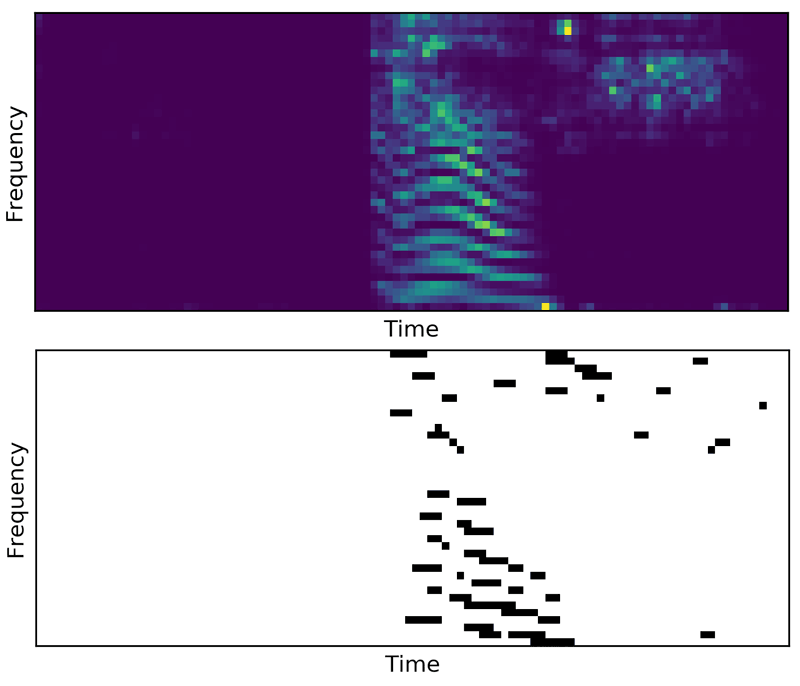
Figure 1. (Top) Example of spectrogram (Mel filters) extracted for the word “off”. (Bottom) Corresponding spike trains for one channel of the first layer.
Conclusion
We firmly believe that these results open a new era for SNNs, in which they will compete with conventional deep learning in terms of accuracy on challenging problems, while their implementation on neuromorphic chips could be much more efficient and use less power.
Link:
[L1] https://github.com/romainzimmer/s2net
References:
[1] S. R. Kheradpisheh and T. Masquelier, “Temporal Backpropagation for Spiking Neural Networks with One Spike per Neuron,” Int. J. Neural Syst., vol. 30, no. 06, p. 2050027, Jun. 2020.
[2] E. O. Neftci, H. Mostafa, and F. Zenke, “Surrogate Gradient Learning in Spiking Neural Networks,” IEEE Signal Process. Mag., vol. 36, no. October, pp. 51–63, 2019.
[3] S. Woźniak, A. Pantazi, T. Bohnstingl, and E. Eleftheriou, “Deep learning incorporating biologically inspired neural dynamics and in-memory computing,” Nat. Mach. Intell., vol. 2, no. 6, pp. 325–336, 2020.
[4] T. Pellegrini, R. Zimmer, and T. Masquelier, “Low-activity supervised convolutional spiking neural networks applied to speech commands recognition,” in IEEE Spoken Language Technology Workshop, 2021.
Please contact:
Timothée Masquelier
Centre de Recherche Cerveau et Cognition, UMR5549 CNRS – Université Toulouse 3, France











