by Nasir Ahmad (Radboud University), Bodo Rueckauer (University of Zurich and ETH Zurich) and Marcel van Gerven (Radboud University)
The success of deep learning is founded on learning rules with biologically implausible properties, entailing high memory and energy costs. At the Donders Institute in Nijmegen, NL, we have developed GAIT-Prop, a learning method for large-scale neural networks that alleviates some of the biologically unrealistic attributes of conventional deep learning. By localising weight updates in space and time, our method reduces computational complexity and illustrates how powerful learning rules can be implemented within the constraints on connectivity and communication present in the brain.
The exponential scaling of modern compute power (Moore’s law) and data storage capacity (Kryder’s law), as well as the collection and curation of big datasets, have been key drivers of the recent deep learning (DL) revolution in artificial intelligence (AI). This revolution, which makes use of artificial neural network (ANN) models that are trained on dedicated GPU clusters, has afforded important breakthroughs in science and technology, ranging from protein folding prediction to vehicle automation. At the same time, several outstanding challenges prohibit the use of DL technology in resource-bounded applications.
Among these issues, the quest for low-latency, low-power devices with on-demand computation and adaptability has become a field of competition. A number of approaches have emerged with candidate solutions to these problems. These include highly efficient hardware specifically designed to carry out the core tensor operations which compose ANN models (especially for mobile devices), cloud-based compute farms to supply on-demand compute to internet-connected systems (held back by access and relevant privacy concerns) and more.
Brain-inspired methods have also emerged within this sphere. After all, the mammalian brain is a prime example of a low-power and highly flexible information processing system. Neuromorphic computing is the name of the field dedicated to instantiating brain-inspired computational architectures within devices. In general, neuromorphic processors feature the co-location of memory and compute, in contrast to traditional von-Neumann architectures that are used by modern computers. Other key features include asynchronous communication of the sub-processors (there is no global controller of the system), and data-driven computation (computing only takes place with significant changes in the input). A number of companies and academic research groups are actively pursuing the development of such neuromorphic processors (Intel’s Loihi, IBM’s TrueNorth, SpiNNaker, and BrainScaleS, to name a few) [1]. These developments progress apace.
We expect that brain-inspired learning rules can become a major driver of future innovation for on-board neuromorphic learning. In particular, the above described architectural design choices for neuromorphic chips precisely match the constraints faced by neurons in brains (local memory and compute, asynchronous communication, data-driven computation and more).
Unfortunately, the computations required to carry out the traditional gradient-based training of ANNs (known as backpropagation of error) break the properties of both neuromorphic architectures and real neural circuits. Error computations in the typical format require non-local information, which implies that the memory distributed across the sub-processing nodes would need to communicate in a global fashion (Figure 1A). For this reason alone, the traditional methods for backpropagation of error are undesirable for neuromorphic “on-chip” training. Furthermore, computations associated with learning and inference (i.e., the application of the ANN) are carried out in separate phases, leading to an undesirable “blocking” phenomenon. By comparison, the brain does not appear to require non-local computations for learning. Thus, by finding solutions to brain-inspired learning, we might arrive at solutions to “on-chip” training of neuromorphic computing.
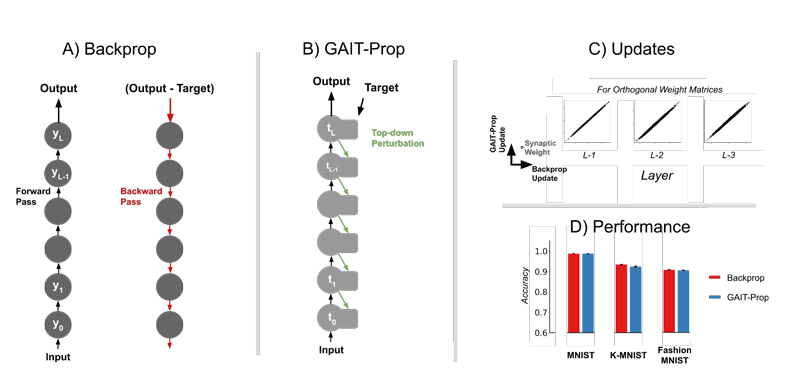
Figure 1: Comparison of standard backpropagation with our proposed GAIT-Prop method. In sections A) and B), circles indicate layers of a deep neural network. A) In backpropagation, all neuron activations yi in each layer i of the network need to be stored during a forward pass, and then the network activity halted so that that weights can be updated in a separate backward pass based on a global error signal. B) In GAIT-Prop, a top-down perturbation circuit is described which can transmit target values ti required to compute weight updates locally at each unit by making use of the dynamics of the system. C) Under particular constraints, GAIT-Prop produces identical weight updates compared to Backprop. D) This is also exhibited during training where on a range of benchmark datasets (MNIST, KMNIST, and Fashion MNIST) GAIT-Prop matches the performance of backpropagation.
Recent developments in brain-inspired learning have produced methods which meet these requirements [2]. In particular, our group recently developed a method (GAIT-Prop [3]) to describe learning in ANN models. GAIT-Prop relies on the same system dynamics during inference and training (Figure 1B) such that no additional machinery is required for gradient-based learning. When the system is provided with an indication of the “desired” output of the system (a training signal), it makes use of theoretically determined inter-neuron connectivity to propagate this desired signal across the network structure through the activities of the network units. The change in activity can then be used by each individual neuron to carry out relevant updates.
Importantly, under some limited constraints, the updates produced by the GAIT-Prop algorithm precisely match those of the very powerful backpropagation of error method (Figure 1C). This ensures that we can achieve matching performance despite the local and distributed nature of the GAIT-Prop algorithm (Figure 1D). Our algorithm also provided for understanding how a desired network output can be translated into target outputs for every node of an ANN system. Since our method relies on error signals being carried within the dynamics of individual units of the network (requiring no specific “error” nodes) it requires less computational machinery to accomplish learning. This feature is ideal for neuromorphic systems as it ensures simplicity of node dynamics while enabling high accuracy.
We see our approach and extensions thereof, in which systems that learn are close to indistinguishable in their dynamics to the systems carrying out inference computations, as an important step in the development of future neuromorphic systems, as it mitigates the complexities associated with standard learning algorithms. Systems equipped with this capability could be embedded in mobile devices and would be capable of learning with data locally, also thereby reducing privacy concerns which are common in an era of cloud-computing and mass data storage.
References
[1] M. Bouvier et al.: “Spiking neural networks hardware implementations and challenges: A survey”, ACM JETC, 2019.
[2] T.P. Lillicrap et al.: “Backpropagation and the brain”, Nat Rev Neurosci, 2020.
[3] N. Ahmad et al.: “GAIT-prop: A biologically plausible learning rule derived from backpropagation of error”, NeurIPS, 2020.
Please contact:
Nasir Ahmad
Radboud University, Nijmegen











