by David Petrosyan (IESL-FORTH)
In order to develop functional devices for quantum computing and analogue and digital quantum simulations, we need controlable interactions between the physical systems representing quantum bits – qubits. We explore strong, long-range interactions between atoms excited to high-lying Rydberg states to implement quantum logic gates and algorithms and to realise quantum simulators of various spin-lattice models to study few- and many-body quantum dynamics.
Quantum systems with many degrees of freedom, such as those composed of many interacting subsystems or particles, are notoriously hard to simulate on classical computers. This is because the Hilbert space for the quantum states of the composite system is exponentially large in the system size, while quantum correlations, or entanglement, between the constituent subsystems often preclude factorisation of the problem into smaller parts. This has led Richard Feynman to suggest, back in 1981, to simulate quantum physics with quantum computers, or universal quantum simulators [1] composed of many quantum two-level systems, like spin-1/2 particles arranged in a lattice, with appropriately controlled couplings between them. In principle, any many-body Hamiltonian dynamics can be decomposed into small time-steps and finite-range interactions between the qubits. This idea has then developed into a general purpose quantum computer which is suitable not only for digital simulations of physical systems, but also for quantum computations. Quantum algorithms for certain mathematical tasks, such as search of unstructured database (Grover) or integer factorisation (Shor), are polynomially or exponentially more efficient than the best known classical algorithms for the same tasks.
Cold atoms trapped in optical lattices or arrays of microtraps represent a scalable architecture to realise quantum computers as well as analogue and digital quantum simulations of many-body dynamics of various spin lattice models. Neutral atoms in the lower electronic states interact very weakly with each other, but when excited to the Rydberg states, their interaction can be very strong over large distances. Rydberg states are highly excited states with the atomic electron placed on an orbit that is far from the ionic core. Due to weak binding of the electron to the ion, the atoms in the Rydberg states are easily polarisable. The resulting long-range interactions between the Rydberg atoms makes them uniquely suited for realising strongly-interacting many-body systems and for implementing various quantum information processing tasks [2].
The interatomic interactions are controllable by lasers that can excite and de-excite the atoms from the non-interacting ground state to the strongly interacting Rydberg state on demand. This has led to proposals to implement quantum logic gates using the switchable interactions, or interaction-induced excitation blockade, between the atoms representing qubits. There have been several experimental demonstrations of the Rydberg quantum gates, but the fidelity of operations has so far been below the threshold value ~0.9999 for a scalable fault-tolerant quantum computation. We study the performance of quantum algorithms under realistic experimental conditions involving noise and imperfections (see Figure 1). We devise novel schemes for high-fidelity quantum logic gates using blockade and resonant exchange interactions between the Rydberg state atoms. This work is being done in collaboration with the theory group of Klaus Mølmer at the Aarhus University and the experimental group of Mark Saffman at the University of Wisconsin—Madison, USA.
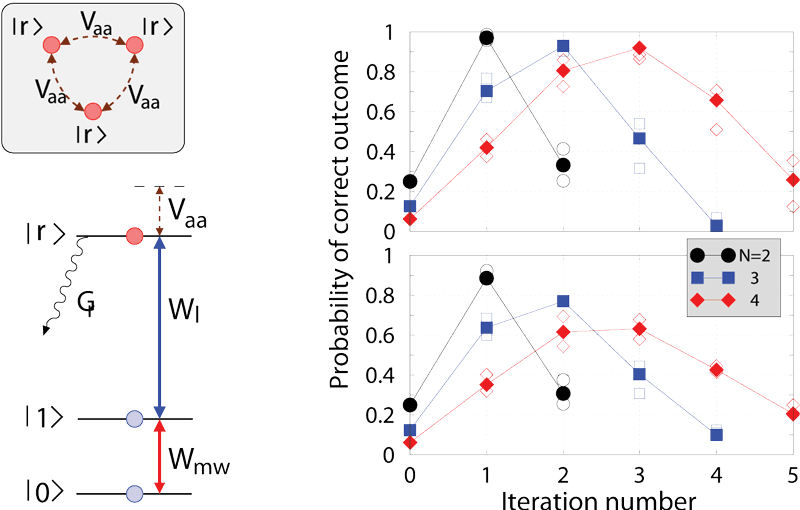
Figure 1: Grover search algorithm with Rydberg blockaded atoms. Left: Level scheme of the register atoms interacting with a microwave field on the qubit transition and with a resonant laser field on the transition to the Rydberg state. Atoms in Rydberg states interact with each other via a strong, long-range potential Vaa which suppresses Rydberg excitation of all but one atom at a time. Right: Probabilities of measuring correct outcomes of the Grover search versus number of iterations, for N=2,3,4 digit quantum register, without (top) and with (bottom) decay of the Rydberg state.
Arrays of trapped atoms excited on demand to the Rydberg states by lasers can realise various spin-lattice models that can serve for both digital and analogue quantum simulations. In addition to switchable interactions, relaxations and energy dissipation can be introduced in this system in a controlled way. We study the dynamics of few- and many-body quantum systems using such Rydberg quantum simulators. As an example, in Figure 2 we show simulations of quasi-crystals of Rydberg excitation as observed in the experiments with laser driven atoms in optical lattices [3]. We collaborate with the theory group of Michael Fleischhauer at the University of Kaiserslautern, Germany, and part of this work is being done within the EU H2020 FET Proactive project RySQ (Rydberg Quantum Simulations) which involves many leading theory and experimental groups in Europe.
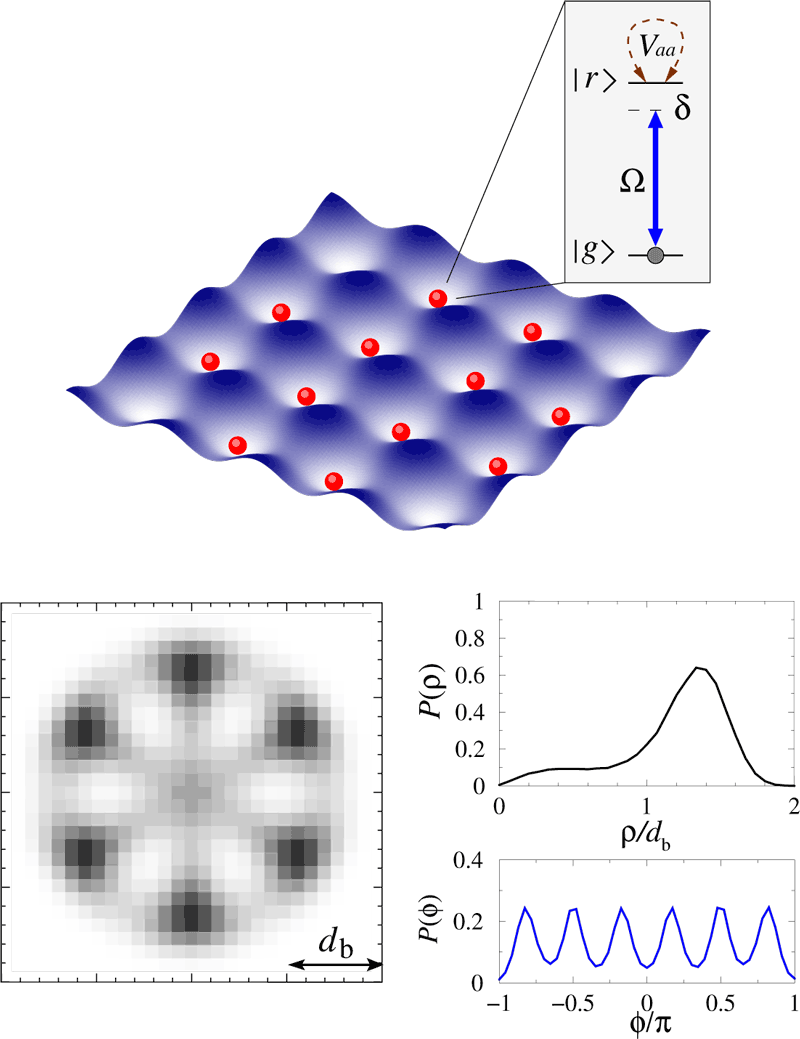
Figure 2: Realising interacting spin lattice models with laser driven atoms. Upper panel illustrates an optical lattice potential for ground state atoms and laser coupling to the strongly interacting Rydberg state. Lower panel shows spatial configuration of six Rydberg excitations, with the axial P(ρ) and angular P(φ) probability distributions, in a 2D disk shaped lattice of 400 atoms driven by a resonant field.
Finally, strong transitions between the Rydberg states of atoms in the microwave frequency range enable their efficient coupling to electrical circuits involving superconducting qubits and resonators. Superconducting qubits can realise fast quantum gates but are less suitable for storage of quantum information. Coupling atoms to solid-state systems permits the realisation of hybrid quantum systems composed of different components with complementary functionalities including quantum information processing, storage and conversion to optical photons for long-distance quantum communication. This is another direction of our research on quantum computation and simulations with Rydberg atoms.
Links:
http://www.quantum-technology.gr/
http://qurope.eu/projects/rysq/
References:
[1] S. Lloyd: “Universal Quantum Simulators”, Science, Vol. 273 (5278), pp. 1073-1078, 1996.
[2] M. Saffman, T. G. Walker, and K. Mølmer, “Quantum information with Rydberg atoms”, Rev. Mod. Phys. Vol. 82, pp. 2313-2363, 2010.
[3] P. Schauß et al., “Crystallization in Ising quantum magnets”, Science Vol. 347 (6229), pp. 1455-1458, 2015.
Please contact:
David Petrosyan
IESL-FORTH, Greece
+30-2810 39 1131











