by Simone Severini (University College London)
Quantum information theory builds bridges between combinatorics, optimisation, and functional analysis.
Nowadays, it is theoretically predicted with paper and pencil, and experimentally demonstrated in the lab, that the physical state of most multi-object quantum mechanical systems cannot be described by looking only at their individual components, and displays stronger-than-classical correlations. In virtue of this point, manipulating some of the components has a global effect on the whole system, even if the components are spatially separated – something expressed by the currently overused and somehow unwelcoming Einstein’s “spooky action at distance”. This phenomenon is known as “entanglement”.
When talking about entanglement, the average mathematical person tends to naturally refrain from alluding to the halo of mysticism surrounding this term, but to focus on the intricate structure of matrices and operators in composite Hilbert spaces. However, while entanglement may appear as a flat consequence of the tensor product used to combine systems as in wave-mechanics, it also has the status of a legitimate and possibly fundamental physical quantity. In truth, its freshly discovered applications range from information-theoretically secure solutions for distributing cryptographic keys to an assortment of remarkable protocols for transmitting information, including superdense coding and teleportation.
Two-player non-local games on graphs have been shown to be a particularly fruitful arena for rigorous research into the power of entanglement and, more generally, the correlations induced by the axiomatic choices leading to their different physical theories. In the proposed framework, two players, Alice and Bob, receive vertices of some graphs. Their task is to respond to questions without knowing each other’s vertices; answers need to satisfy a certain property as a function of the received vertices. Depending on the type of correlations displayed by the physical world of Alice and Bob, this situation suggests a collection of new graph parameters, which are captured by rich mathematical structures, and give an occasion to generalise graph theory ideas to functional analysis. One of these quantities is now called quantum chromatic number and it is known to be loosely upper bounded by the more familiar chromatic number – when, in the non-local game, answers need to be different for adjacent and equal for identical vertices. The quantum chromatic number was the first quantum graph parameter to be studied. Such research direction has eventually ramified into multiple routes. A brief account of the salient points follows.
In 1956, Shannon defined the zero-error capacity of a communication channel as the largest rate at which information can be transmitted over the channel with error probability zero. The notion has contributed to fuel a great amount of research in semidefinite programming and structural graph theory. Berge’s perfect graphs were remarkably motivated by the zero-error capacity and the Lovász theta function was introduced as an upper bound. When the parties can share and locally manipulate entangled states, the analogue capacity has also been proved to be bounded by Lovász theta, but to be exponentially larger in various single-shot and asymptotic cases [1, 2]. Given the link between zero-error capacity and the problem of transmitting data over a broadcast channel (e.g., coaxial cable or satellite), this result highlights a prospective quantum advantage exploitable in real-world communications.
In 1976, Connes casually formulated a conjecture about a fundamental approximation property for finite von Neumann algebras – the Connes embedding problem. Over time, many unexpected equivalent statements for the conjecture have emerged. A hierarchy beyond the quantum chromatic number has led to a novel reformulation of the Connes conjecture, and generated a fresh effort towards its solution [L1]. The new approach is centred on combinatorial ideas lifted to the realm of operator algebras. Moreover, extending this mathematical landscape, hierarchies of quantum graph parameters associated to correlations can be placed in the framework of (tracial noncommutative) polynomial optimisation [L2]
In 1993, Tsirelson proposed some problems concerned with deciding whether the axiomatic mathematical models of non-relativistic quantum mechanics, where observers have operators acting on a finite dimensional tensor product space, and algebraic quantum field theory, where observers have commuting operators on a (possibly infinite dimensional) single space, produce the same set of correlations. A 2016 breakthrough, based on geometric group theory, settled the “middle” Tsirelson problem, by observing that the set of (tensor-product) quantum correlations is not closed [L3]. Interestingly, a successive alternative proof of this result makes use of quantum graph parameters [L4].
This new technical machinery became further consolidated via a quantum version of graph homomorphism, a familiar but powerful generalisation of graph colouring. This new technical machinery became further consolidated via a quantum version of graph homomorphism, a familiar but powerful generalisation of graph colouring. The new type of homomorphism suggested relaxations of graph isomorphism to settings corresponding to various physical theories. The findings of this line of research are surprising. While fractional isomorphism corresponds to sharing some type of correlations stronger than entanglement – hence, it gets an operational interpretation, – quantum isomorphism is obtained by relaxing the integer programming formulations for standard isomorphism to Hermitian variables [3] (see Figure 1).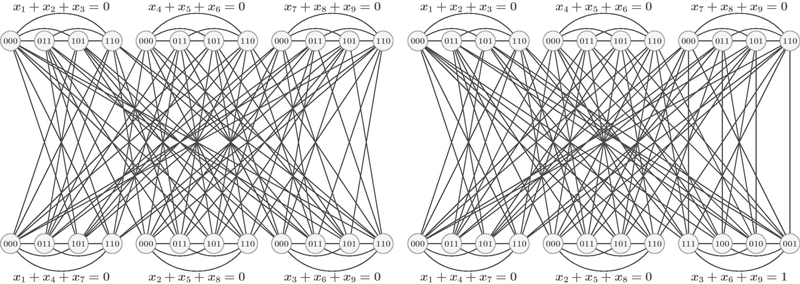
Figure 1: Two graphs on 24 vertices that are quantum isomorphic but not isomorphic. The construction is related to the FGLSS reduction from inapproximability literature, as well as the CFI construction.
Some members of the Quantum Computing, Information, and Algebras of Operators (QCIAO) collective (lecturers of the LMS Research School Combinatorics and Operators in Quantum Information Theory, Belfast September 2016).
The QCIAO Collective is an international collaboration focused on the topics of this article [L5].
Links:
[L1] https://arxiv.org/abs/1503.07207
[L2] https://arxiv.org/abs/1708.09696
[L3] https://arxiv.org/abs/1606.03140
[L4] https://arxiv.org/abs/1709.05032
[L5] http://www.qciao.org/
References:
[1] R. Duan, S. Severini, A. Winter: “Zero-error communication via quantum channels, non-commutative graphs and a quantum Lovasz theta function”, IEEE Trans. Inf. Theory 59(2):1164-1174, 2013.
[2] J. Briët, H. Buhrman, D. Gijswijt: “Violating the Shannon capacity of metric graphs with entanglement”, PNAS 2013 110 (48) 19227-19232.
[3] A. Atserias, et al.: “Quantum and non-signalling graph isomorphisms”, ICALP 2017.
Please contact:
Simone Severini
University College London, UK
+44 (0)20 3108 7093











