by Nicolas Augier (École polytechnique), Ugo Boscain (CNRS) and Mario Sigalotti (Inria)
The dynamics of a quantum mechanical system is described by a mathematical object called Hamiltonian. The possible results of an energy measure are known as the “eigenvalues” (or energy levels) of the Hamiltonian. After an energy measure, the system collapses into a particular state called the eigenstate corresponding to the measured energy. Adding corners to adiabatic paths can be used to generate superpositions of eigenstates with simple and regular control laws.
The goal of quantum control is to design external fields (the controls) whose action induces a prescribed transition between two states of a quantum system.
A widely used technique is based on the principle of adiabatic evolution: If the initial condition is an eigenstate of the controlled Hamiltonian (i.e., the Hamiltonian including the external field) and the variation of the external fields is slow, then the state of the system stays close to the instantaneous eigenstate (namely, the eigenstate of the controlled Hamiltonian with frozen time).
Adiabatic evolution works as described when the energy levels of the controlled Hamiltonian satisfy a gap condition, which means that they stay away from one from another and in particular they do not intersect. The theory can be extended to systems presenting eigenvalue intersections. When the intersection of two eigenvalues is transversal and the initial condition corresponds to the lower eigenvalue then, after the intersection, the trajectory adiabatically follows the eigenstate corresponding to the upper eigenvalue.
One is typically interested in adiabatic paths for which the controls start and end at zero. Such controls may be used to induce nontrivial transitions only if there exist paths in the space of controls that are not passing back and forth through the same intersections. This is why such an adiabatic setup makes sense for control purposes only when the controls have more than one degree of freedom.
In the general case one looks at the singular set, i.e., the set of all control values for which the Hamiltonian has degenerate eigenvalues. The applicability of the adiabatic strategy relies on the fact that the singular set does not disconnect the set of available control parameters. Such a disconnection is very rare, however, in the sense that for a generic system the singular set has codimension 3 for complex Hamiltonians and codimension 2 for real ones.
Figure 1 shows the eigenvalues of a 3-level quantum system driven by two controls in the well-known STIRAP configuration. In this case there are two eigenvalue intersections: one between the first and the second levels (on the axis where the first control is zero) and one between the second and the third levels (where the second control vanishes). Notice that the resulting adiabatic strategy follows the famous counter-intuitive pattern, meaning that one first activates the control associated with the transition between the second and the third energy levels and then the one associated with the transition between first and the second ones, with an overlap between the two pulses [1].

Figure 1: The eigenvalues of a 3-level quantum system driven by 2 controls in the STIRAP configuration.
The technique explained above provides a simple strategy to induce a transition between any two eigenstates of the free Hamiltonian, under the assumption that all energy levels intersect.
In collaboration with Francesca Chittaro (Toulon University) and Paolo Mason (CNRS, CentraleSupelec) we have developed a technique to create superpositions between eigenstates using broken adiabatic paths [2].
The principle of our approach is that if an adiabatic path reaches a point in the singular set and makes there a corner, then the state splits partially on the lower energy level and partially on the upper one. Modulating the entry and exit direction, hence the angle between the two, one can arbitrarily select the occupation of the two energy levels. Such an idea makes it possible, starting from an eigenstate, to reach any superposition of eigenstates whose corresponding eigenvalues intersect [3].
Figure 2, for a 3-level system, shows a broken adiabatic path inducing a transition from the first energy level to a superposition of the first and the third energy levels. Given the desired population levels at the final time, it is possible to compute the angle between the entry and exit direction at the corner in order to induce a transition to a state having such population levels. In the picture, we show for instance a control inducing a transition from an eigenstate corresponding to the first eigenvalue to a superposition with equal weights between the first and the third eigenstates, with no population on the second energy level.
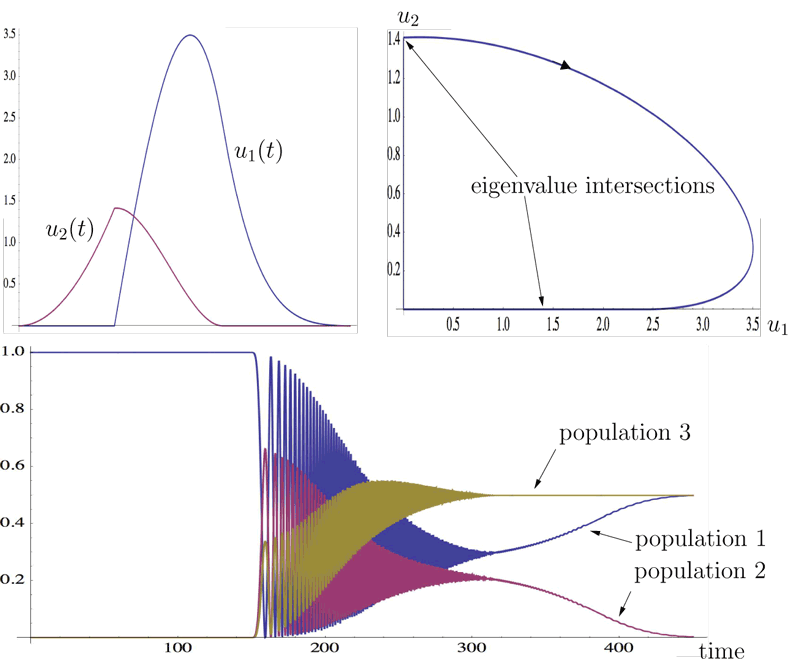
Figure 2: A broken adiabatic path inducing a transition from the first energy level to a superposition of the first and the third energy levels.
The project is supported by the ERC starting grant GECOMETHODS (2010-2016) and by the French ANR projects GCM (2009-2013). Extensions and algorithmic refinements are under study in the framework of the Inria team CAGE thanks to the support of the French ANR project QUACO (2017-2021).
References:
[1] C.E. Carroll and F.T. Hioe: “Analytic solutions for three-state systems with overlapping pulses”, Phys. Rev. A, vol. 42, pp. 1522-1531, 1990.
[2] U. Boscain et al.: “Adiabatic control of the Schrödinger equation via conical intersections of the eigenvalues”, IEEE Trans. Autom. Control, vol. 57, pp. 1970-1983, Aug. 2012.
[3] U. Boscain et al.: “Approximate controllability, exact controllability, and conical eigenvalue intersections for quantum mechanical systems”, Commun. Math. Phys, vol. 333, pp. 1225-1239, Feb. 2015.
Please contact:
Nicolas Augier, CMAP, École polytechnique, France
Ugo Boscain, CNRS, LJLL, Université Pierre et Marie Curie, France
Mario Sigalotti
Inria, LJLL, Université Pierre et Marie Curie, France











