by Aleks Kissinger (Radboud University)
String diagrams provide a powerful tool for uncovering hidden algebraic structure in quantum processes. This structure can be exploited to optimise quantum circuits, derive fault-tolerant computations, and even probe the foundations of physics.
Quantum computers have the ability to reshape the modern world, offering huge computational speed-ups for a wide variety of problems in mathematics, physics, chemistry, and computer science. However, the existing and emerging quantum computational devices face stringent limitations in memory, computational power, and tolerance to noise, making it crucial to develop sophisticated techniques for optimising the software which drives these systems. Quantum circuits have become the de facto “assembly language” for quantum software. They describe computations in terms of a series of primitive operations, called quantum gates, performed on a register of quantum bits (qubits), which is then measured to give a result. While quantum gates are useful as building blocks for computations, they lack a well-understood algebraic structure, making it difficult to understand when two circuits are equivalent (i.e., describe the same computation) or to transform one circuit into another for the sake of optimisation or fault-tolerance.
In 2008, researchers at Oxford University produced a unique solution to this problem: the ZX-calculus. Originally developed as an abstract method for studying the behaviour of complementary observables in quantum mechanics (indeed the ‘Z’ and ‘X’ refer to the complementary Pauli observables of the same name), the ZX-calculus quickly showed itself to be a useful practical language for reasoning about quantum circuits, as well as other qubit-based models of computation, such as measurement-based quantum computation. The ZX-calculus works by decomposing quantum gates into even more primitive components, called “spiders” (Figure 1). These basic pieces satisfy a small number of algebraic laws, which in turn yield a great deal of power. For example, the four laws shown in Figure 2 suffice to transform any two equivalent Clifford quantum circuits into the same circuit. Clifford circuits are a well-studied class of circuits which can be simulated efficiently on a classical computer, so it may not be too surprising that the ZX-calculus gives an easy, algebraic handle on circuit equivalence. However, what is surprising is that groups in Oxford and LORIA (a research unit affiliated with ERCIM member Inria) have shown in recent months that an extension to these rules can decide equality for Clifford+T circuits [1] and even a fully universal family of quantum circuits [2]. These families of circuits are capable of producing any quantum computation imaginable (or, in the case of Clifford+T, approximating it to arbitrarily high precision). Thus, a complete algebraic characterisation of equivalence for these circuits is a major breakthrough.
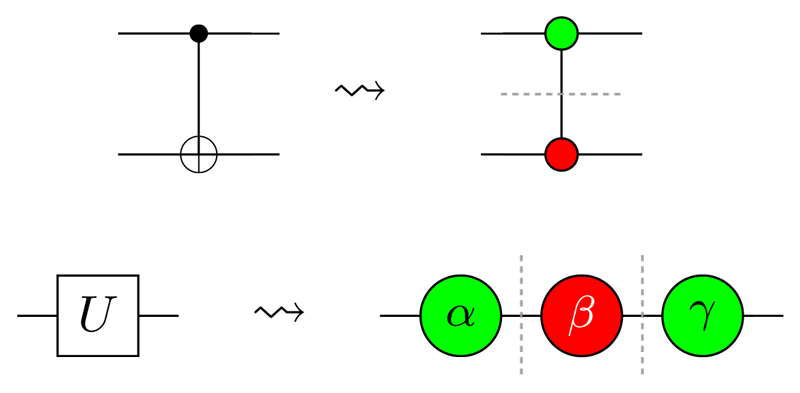
Figure1: Decomposing quantum gates into more primitive pieces called “spiders”.

Figure 2: The rules of the ZX-calculus, which suffice to derive all equations that hold between Clifford circuits.
The ZX-calculus—including the extensions proposed by the Oxford and LORIA groups—is based on string diagrams, which can be seen as a sort of generalisation of quantum circuits. They first appeared in the work of Penrose in the 1970s, and since then have been applied to a broad range of applications in physics and computer science, including tensor networks in high-energy physics, signal-flow graphs, electrical and electronic circuits, computational linguistics, and concurrent computation. Earlier this year, Coecke and Kissinger published a textbook which gives a comprehensive introduction to quantum theory, quantum computation, and quantum foundations purely in the language of string diagrams [3].
String diagrams not only provide a unique and intuitive way to introduce the core concepts of quantum theory, but also a dramatically different way of working with quantum mechanical processes. Within the diagrammatic approach to quantum theory (a.k.a. “Categorical Quantum Mechanics”, see link [L2]), concepts such as connectivity, composition, and interaction take centre stage, whereas concrete Hilbert-space calculations are secondary. For example, foundational questions around quantum non-locality and quantum causal structure can be posed in terms of whether a diagram decomposes in a certain way across time and space, and what consequences that decomposition has on our observations.
More pragmatically, quantum algorithms and communication protocols can be proven correct using diagram transformation rules, even in cases involving far too many qubits for concrete calculation. To assist with producing, checking, and sharing these proofs, researchers at Radboud University, University of Strathclyde, and Oxford have developed a tool called Quantomatic (Figure 3). Quantomatic is a “proof assistant for diagrammatic reasoning”. Using a combination of human-guided diagram transformations and automated rewrite strategies (programmable in a Python-based strategy language), it is possible to perform a variety of tasks in Quantomatic, such as optimising small to medium-sized quantum circuits, verifying multi-party communication protocols, and computing encoded logical operations within certain families of quantum error correcting codes.
![Figure 3: Quantomatic, a proof assistant for diagrammatic reasoning. Here, it is computing a transversal implementation of a CCZ gate within a quantum error correcting code (namely, the [[8,3,2]] colour code; see links [L1] and [L3] for more details).](/images/stories/EN112/kissinger3.png)
Figure 3: Quantomatic, a proof assistant for diagrammatic reasoning. Here, it is computing a transversal implementation of a CCZ gate within a quantum error correcting code (namely, the [[8,3,2]]colour code; see links [L1] and [L3] for more details).
The teams in Nijmegen, Oxford, LORIA, and Strathclyde, with the help of collaborators at LRI, Durham, and the UK’s NQIT Quantum Hub, are now aiming to produce fully automated techniques for circuit optimisation, scale up to large computations on hundreds of logical qubits (with error correction), and develop new kinds of transformation procedures to work within the constraints of first-generation quantum hardware, such as limited topologies for qubit interactions and distinguished gate- vs. memory-optimised physical qubits.
Links:
[L1] http://quantomatic.github.io
[L2] http://cqm.wikidot.com
[L3] https://kwz.me/hB7
References:
[1] E. Jeandel, S. Perdrix, R. Vilmart: “A Complete Axiomatisation of the ZX-Calculus for Clifford+T Quantum Mechanics”, Preprint, arXiv:1705.11151. 2017.
[2] K. Ng, Q. Wang: “A universal completion of the ZX-calculus”, Preprint, arXiv:1706.09877. 2017.
[3] B. Coecke, A. Kissinger: “Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning”, Cambridge University Press. 2017.
Please contact:
Aleks Kissinger
iCIS Radboud Universiteit, The Netherlands











