by Alain Sarlette (Inria) and Pierre Rouchon (MINES ParisTech)
Despite an improved understanding of the potential benefits of quantum information processing and the tremendous progress in witnessing detailed quantum effects in recent decades, no experimental team to date has been able to achieve even a few logical qubits with logical single and two qubit gates of tunably high fidelity. This fundamental task at the interface between software and hardware solutions is now addressed with a novel approach in an integrated interdisciplinary effort by physicists and control theorists. The challenge is to protect the fragile and never fully accessible quantum information against various decoherence channels. Furthermore, the gates enacting computational operations on a qubit do not reduce to binary swaps, requiring precise control of operations over a range of values.
The major issue for building a quantum computer is thus to protect quantum information from errors. The quantum counterpart of error correcting codes provides an algorithmic solution, based on redundant encoding, towards scaling up the precision in this context. However, it first requires technology to reach a threshold at which the hardware achieves the following on its own:
- all operations, in any big system, must already be accurate to a very high precision;
- the remaining errors follow a particular scaling model, e.g., they are all independent in a network of redundant qubits.
Under these conditions, adding more physical degrees of freedom to encode the same quantum information keeps leading to better protection. Otherwise, the fact that new degrees of freedom and additional operations also carry new possibilities for inducing errors or cross-correlations, can degrade the overall performance.
In the QUANTIC lab at Inria Paris [L1], we are pursuing a systems engineering approach to tackle this issue by drawing inspiration from both mathematical control theory and the algorithmic error correction approach (Figure 1).
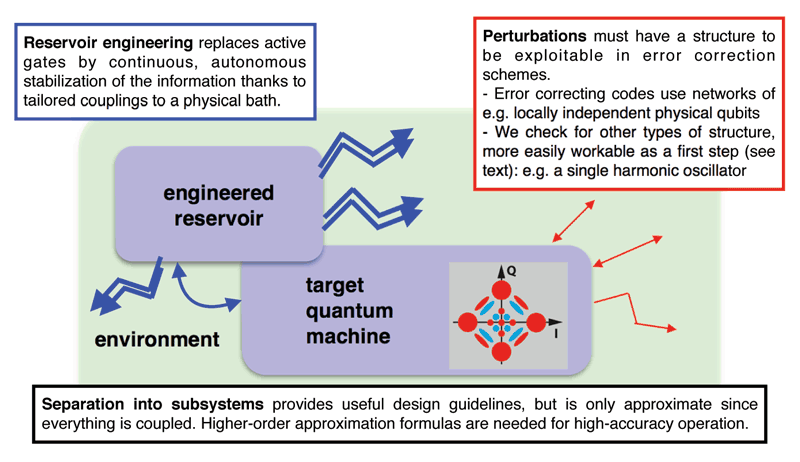
Figure 1: General scheme of our quantum error correction approach via “hardware shortcuts”. The target “quantum machine” is first embedded into a high-dimensional system that may have strong decoherence, but only along a few dominating channels (red). Then, a part of the environment is specifically engineered and coupled to it in order to induce a strong information-stabilising dissipation (blue). This entails stabilising the target quantum machine into a target subspace, e.g., “four-legged cats” of a harmonic oscillator mode; and possibly, replacing the measurement of error syndromes and conditional action, by a continuous stabilisation of the error-less codewords. Development of high-order model reduction formulas is needed to go beyond this first-order idea and reach the accuracies enabling scalable quantum information processing.
A first focus of the group is to design a hardware basis where a large Hilbert space for redundant encoding of information comes with just a few specific decoherence channels. Concentrating efforts on rejecting these dominant noise sources allows more tailored and simple stabilising control schemes to be applied to improve the quality of these building blocks towards more complex error correction strategies. Such hardware efficiency is typically achieved when many energy levels are associated to one and the same physical degree of freedom. A prototypical example is the “cat qubit”, where information about a single qubit is redundantly encoded in the infinite-dimensional state space of a harmonic oscillator, in such a way that the dominant errors reduce to the single photon loss channel; and this error is both information-preserving and non-destructively detectable. This overcomes the need for tracking multiple local error syndromes and applying according corrections in a coupled way, as would be the case for a logical qubit encoded on a network of spin-1/2 subsystems. An implementation of this principle in superconducting circuits has recently achieved the first quantum memory improvement thanks to active error correction.
A second point of attention is the speed of operations. Indeed, quantum operations take place at extremely fast timescales — e.g., tens of nanoseconds in the superconducting circuits favoured by several leading research groups. This leaves little computation time for a digital controller acting on the system. Conversely, it hints at the fact that a smartly designed quantum system could stabilise fast on its own onto a protected subspace, possibly in combination with a few basic control primitives. Such autonomous stabilisation can be approached by a “reservoir engineering” strategy, where conditions are set up for dissipation channels to systematically push the system into a desired direction. This can enact e.g., fast reset of qubits, or error decoding and correction, all in one fast and continuously operating (“pumping”) hardware without any algorithmic gates. Such “reservoir engineering” also plays an important role in effectively isolating quantum subsystems with particularly concentrated error channels, thus in creating the conditions of the previous paragraph.
This brings us to the more mathematical challenges. The design of engineered reservoirs, such as the singling out of a “quantum machine” from its environment, is based on approximations where weak couplings are neglected with respect to dominant effects. These approximations enable tractable systems engineering guidelines to be derived — rather than having to treat a single big quantum bulk, whose properties are one target of the quantum computers themselves. Current designs are based on setting up systems with first dominant local effects. This has to be improved and scaled up to reach the requirements 1. and 2., since every control scheme can only be as precise as its underlying model. We are therefore launching a concrete effort towards high-precision model reduction formulas, together with the superconducting circuit experimentalists to identify typical needs, but with a general scope in mind. Preliminary work already shows the power of higher-order formulas in identifying design opportunities (Figure 1), paving the way to improved “engineered” hardware for robust quantum operation.
Link:
[L1] https://www.inria.fr/en/teams/quantic
References:
[1] M. Mirrahimi, Z.Leghtas et al: “Dynamically protected cat-qubits: a new paradigm for universal quantum computation”, New Journal of Physics, 2014.
[2] N. Ofek et al.: “Extending the lifetime of a quantum bit with error correction in superconducting circuits”, Nature, 2016.
[3] J. Cohen: “Autonomous quantum error correction with superconducting qubits”, PhD thesis, ENS Paris, 2017.
Please contact:
Alain Sarlette, Pierre Rouchon, Inria
+ 33 1 80 49 43 59











