by Gábor Ivanyos and Lajos Rónyai (MTA SZTAKI, Budapest)
Effective versions of some relaxed instances of the Chevalley-Warning Theorem may lead to efficient quantum algorithms for problems of key practical importance such as discrete logarithm or graph isomorphism.
The Theory of Computing Research Group of the Informatics Laboratory at MTA SZTAKI has expertise in algebraic aspects of quantum computing, including quantum algorithms for algebraic and arithmetical problems, as well as application of algebraic methods as ingredients of quantum algorithms. Some of our projects aim at discovering hidden algebraic structures, e.g., symmetries of certain objects. A main example is the so-called “hidden subgroup problem”, which includes such prominent special cases as the task of computing discrete logarithms and the question of finding isomorphisms of graphs. The object we are given is a function f defined on a large finite group G and we are looking for the subgroup H consisting of all elements h for which f(xh) = f(x) for every x from G. In other words, H is the group of elements whose action leaves f invariant. (We remark note that in most cases, we further require that f is such that f(x) = f(y) if and only if y = xh for some h from H.) Perhaps the simplest and best known example of this is finding periods for functions defined on the integers. One of the greatest successes of quantum algorithms, Shor’s method for factoring integers, is based on finding such a period. Computing discrete logarithms in various settings are is also an instance of the hidden subgroup problem over abelian groups.
The graph isomorphism problem can be cast as an instance of the hidden subgroup problem over a noncommutative group G. In contrast with the commutative case, for which efficient quantum algorithms are known, the complexity of the noncommutative hidden subgroup problem has remained open even for certain groups that are very close to commutative ones. Among the few positive results in this direction, we mention our polynomial time algorithm, developed in a joint work [1], which finds hidden subgroups in a fairly wide class of groups in which the order of the elements is bounded by a constant. The overall progress is much more modest even in “so-called two-step solvable groups” (these are in a certain sense composed of two commutative groups) in which elements of larger order are present.
With our collaborators we found [2] that the hidden subgroup problem for a subclass of such groups can be further generalised to another class of problems regarding hidden algebraic structure. In this class, the hidden object is a polynomial map between vector spaces over a finite field. Certain hidden subgroup problems can be formulated as hidden polynomial map instances (there is a reduction in the other direction as well, but this results in a bigger hidden subgroup problem). A simple illustrative example of a hidden polynomial map is as follows: let f(X) be an unknown univariate polynomial of constant degree. We have access to a quantum oracle which returns E(Y2-f(X)) for given pairs (X,Y). Here E is an unknown injective encoding of the field. The task is to determine f (up to constant term). We developed [2,3] a polynomial time quantum algorithm for finding such hidden polynomial maps under the assumption that they have constant degree.
One of the critical ingredients of our quantum algorithm is a classical algorithm that under certain conditions finds a nontrivial solution of a system of polynomial equations of a very special kind, for which the basic and famous Chevalley-Warning theorem of number theory ensures the existence of a nontrivial solution. Our system is obtained from a system of homogeneous linear equations by replacing each variable by its d-th power where d is a fixed positive integer:
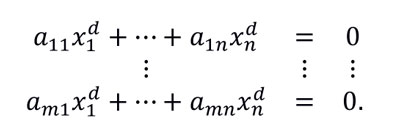
The condition that allowed us a method running in polynomial time is that the number of variables, compared to the number of equations and the degree d, is sufficiently large. (Here by polynomial time we mean time bounded by a function polynomial in the bit size of the array of the coefficients, which is the number of equations, m, times the number of variables, n, times the logarithm of the size of the base field). In the quantum setting in which our algorithm is applied, the degree is essentially the degree of the hidden polynomial map and the number of equations is related to the dimension of the underlying spaces, while we are allowed to choose the number of variables. (Note however, that the system is not required to be sparse, the n times m array of the coefficients can be arbitrary.)
Observe that without any assumption on the number n of variables, already over the field consisting of three elements the quadratic case of the problem becomes NP-hard. This can be shown by a modification of the standard reduction of SAT to Subset sum. (In fact, that case of the problem is just finding a zero-one solution of the corresponding linear system.) On the other hand, from the Chevalley-Warning Theorem it follows that if n > md, then our system always has a nontrivial solution. Then an interesting question arises: how hard is it to find a nontrivial solution? There is some evidence (such as the above mentioned hardness result) that this question is too difficult when the number of variables is close to the Chevalley-Warning bound md. For this reason, we look for an efficient solution for relaxations in which n is substantially larger than this bound. First, it is worth noting that by a simple and natural recursive algorithm, it is easy to find a solution in polynomial time, when the number n of variables is greater than a function like d raised to the m-th power. This method is useful when m is constant. What can we say when d is kept constant? For this variant of the problem, we have developed a much more sophisticated algorithm [3]. This result is probably not optimal and an improvement could be a first step toward quantum algorithms for finding hidden polynomial maps of higher degree and toward hidden subgroup algorithms in some more complex groups.
References:
[1] K. Friedl, et al: “Hidden translation and translating coset in quantum computing” SIAM Journal on Computing 43 (2014), pp. 1-24.
[2] T. Decker, et al.: “Polynomial time quantum algorithms for certain bivariate hidden polynomial problems”, Quantum Information and Computation 14 (2014), pp. 790-806.
[3] G. Ivanyos, M. Santha: “Solving systems of diagonal polynomial equations over finite fields,” Theoretical Computer Science 657 (2017), pp. 73-85.
Please contact:
Gábor Ivanyos and Lajos Rónyai
MTA-SZTAKI, Hungary











