by Christophe De Vleeschouwer (UCL) and Isabelle Migeotte (ULB)
The progress in imaging techniques has allowed the study of various aspects of cellular mechanisms. Individual cells in live imaging data can be isolated using an elegant image segmentation framework to extract cell boundaries, even when edge details are poor. Our approach works in two stages. First, we estimate interior/border/exterior class probabilities in each pixel, using binary tests about fluorescence intensity values in the pixel neighbourhood and semi-naïve Bayesian inference. Then we use an energy minimisation framework to compute cell boundaries that are compliant with the pixel class probabilities.
Progress in embryo culture and live imaging techniques has allowed direct observation of cellular rearrangements in embryos from various species, including those with internal development. The images collected using fluorescence microscopy in this context exhibit many characteristics that make segmentation challenging. These include limited contrast and marker diffusion, resulting in poor membrane details. Moreover, the inner textures of distinct cells present quite similar statistics, making clustering-based segmentation inappropriate (see Figure 1).
![Figure 1: Annotated ground-truth (top-left), and segmentation results for Mean-Shift, Felzenszwalb et al. (see [1] for references), and our approach.](/images/stories/EN108/de_vleeschouwer.png)
Figure 1: Annotated ground-truth (top-left), and segmentation results for Mean-Shift, Felzenszwalb et al. (see [1] for references), and our approach.
To circumvent those limitations, we propose to adopt a two-stage approach. In an initial stage, we learn how cell interior pixels differ from exterior or border pixels. Then we adopt a global energy minimisation framework to assign cell-representative labels to pixels, based on their posterior interior/border/exterior class probabilities. It was critical to explicitly consider a class of pixels lying on borders between adjacent cells since, in previous work on this dataset, the main problem we encountered was splitting cellular aggregates into individual cells.
Formally, we use a semi-Naive Bayesian approach to estimate the probabilities that each pixel lies: (i) inside a cell, (ii) on a boundary between adjacent cells, and (iii) in the background, exterior to a cell. In practice, those probabilities are estimated based on the realisation of a number of binary tests, each test being defined to compare the intensity of two pixels whose position has been drawn uniformly at random within a square window centred on the pixel of interest [1]. We have chosen semi-Naive Bayesian estimation because it has been shown to be accurate and offer good robustness and generalisation properties in many vision classification tasks [2]. This last point is important since the manual definition of cell contour ground-truth is generally considered as a tedious task, which practically limits the number of training samples.
The estimation of the inner, boundary, and exterior class probabilities for each pixel is, however, not sufficient to properly segment the cells. Indeed, as shown in Figure 2, the pixel classification resulting from the application of the argmax operator to those three probability values does not provide accurate cell segmentation. To exploit the probabilities in a spatially consistent manner, we turn the segmentation problem into a pixel-to-label assignment problem. Therefore, a set of labels is first defined in a way that ensures that each cell is represented by at least one label. In practice, each label is associated with a segmentation seed, defined to be the centre of a connected set of pixels whose interior class probability lies above a threshold, as represented by red dots in Figure 2. To circumvent the threshold selection issue, and to adapt the seed definition to the local image contrast, we consider a decreasing sequence of thresholds. Large thresholds result in small segments that progressively grow and merge as the threshold decreases. Among those segments, we only keep the largest ones whose size remains (significantly) smaller than the expected cell size. This might result in multiple seeds per cell, as depicted in Figure 2. A unique label is then attached to each seed, adding one virtual label for the background. The fact that a single cell induces multiple seeds, and thus multiple labels, is not dramatic since the subsequent energy-minimisation has the capability to filter out redundant labels.
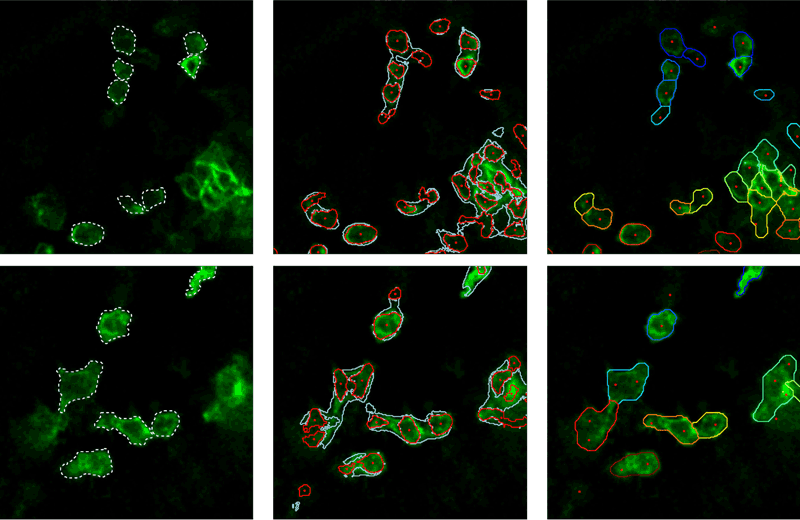
Figure 2: Ground-truth (left column), argmax classification (middle), and pixel-to label assignment (right).
Given a set of n labels L = {1,…,n}, we are looking for a pixel-to-label assignment vector f that minimises the energy
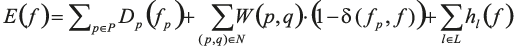
In this equation, the first term favours the assignment to pixel p of a label fp=f(p) that corresponds to a seed that can be connected to p without crossing a boundary or an exterior area. Formally, we define
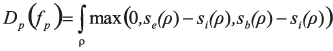
with ρ denoting the shortest path between the pixel p and the seed associated to label fp. The scores se, sb, and si are defined as the logarithm of the posteriors estimated in a pixel position based on the random ferns.
The two additional terms regularise the pixel-to-label assignment. In the second term, δ(.,.) denotes the Kronecker delta, and W(p,q) is defined to induce large values when neither p nor q have a high probability of being on a border between two cells. Formally,
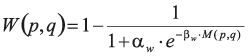
and

Hence, this second term favours short borders passing through pixels that have a large boundary probability.
The third term hl(f) induces a (constant) penalty when the assignment f uses label l, thereby favouring assignments that use a small number of labels, which tends to merge seeds when it is relevant from the probability distribution point of view.
To solve this energy-minimisation framework, we rely on the fast approximate minimisation with label costs introduced by Delong et al (see reference in [1]). The right column in Figure 2 presents the segmentation resulting from our proposed energy minimisation. We observe that the regions extracted are in very good agreement with the ground truth depicted in the left column as a dashed white line. In contrast to conventional algorithms (see Figure 1), our segmentation procedure is able to accurately localise boundaries between touching cells. Moreover, our method is also able to merge multiple seeds within a unique region or to reject seeds situated in the background when they are not supported by the probability distribution. In conclusion, our work appears to be an elegant, versatile and effective solution to exploit posterior interior/border/exterior probability maps in a segmentation context. Once detected, cells can be tracked using dedicated multi-object tracking algorithms, as outlined in [3].
References:
[1] A. Browet, et al.: “Cell segmentation with random ferns and graph-cuts”, IEEE International Conference on Image Processing 2016, http://arxiv.org/abs/1602.05439.
[2] P. Parisot, C. De Vleeschouwer: “Scene-specific classifier for effective and efficient team sport players detection from a single calibrated camera”, Computer Vision and Image Understanding, Special Issue on Computer Vision in Sports, 2017.
[3] Amit K.C., C. De Vleeschouwer: “Discriminative Label Propagation for Multi-Object Tracking with Sporadic Appearance Features”, Int. Conf. on Computer Vision (ICCV), Sydney, Australia, 2013. Extended version to appear in IEEE Trans. on Pattern Analysis and Machine Intelligence, 2017.
Please contact:
Christophe De Vleeschouwer
Université catholique de Louvain, Belgium
Isabelle Migeotte
Université libre de Bruxelles











