by Petr Pecha, Miroslav Kárný, Emilie Pechová, Václav Šmídl and Ondřej Tichý (Institute of Information Theory and Automation)
A research team from the department of Adaptive Systems of ÚTIA [L1] has solved the project HARP [L2] which included examination of various release scenarios under worst-case meteorological conditions. Recently, the team has been focused on inspection of the calm situations characterised by stable atmosphere at very low wind speed with possibility of rainfall. Although the probability of such episodes is low, possible radiological impact on the environment can be serious. Developed methodology supports deployment of the sampling-based methods for probabilistic estimation of the radiological impact of radiation accidents.
Accidental discharges of radioactive substances from an elevated source into the motionless (calm) atmosphere are examined with the aim to quantify possible radiological impact on the population. In a few hours of a calm meteorological situation, a significant level of radioactivity may accumulate around the source. The inspected scenario assumes that the calm situation expires and a wind-induced convective movement of the air immediately begins. Randomness of the model parameters of this CALM scenario allows generation of complex random radiological trajectories. They constitute the deposition of radionuclides on the ground during both calm and convective stages of the release [1]. Their inspection is the necessary prerequisite for the prospective uncertainty and sensitivity analyses.
Speedup based on the new “super-puff” concept
The radioactive release from an elevated source into the motionless ambient atmosphere is approximated by a long sequence of discrete discharges (instantaneous puffs) described by 3-D Gaussian-puff formulae. Each puff has a shape of an expanding discus with its centre at the pollution source. The puff distribution describes the radioactivity concentration in air released at effective height. The radioactivity depletion from the air caused by physical mechanisms of radioactive decay, dry depletion and wet depletion is implemented. Demands on computing resources are substantially decreased by projecting the non-Gaussian sum (red line in Fig. 1) of all partial puffs (blue lines in Fig. 1) on one representative Gaussian “super-puff” distribution. This approximation based (AB) solution uses the projection approach implied by Bayes’ paradigm [2]. Benefit of the reduced computational load is evident, especially for a large number of puffs M. It requires only one-shot run modelling of the ensuing convective transport, which significantly lowers prospective demands on necessary application of more powerful but laborious dispersion codes. The brute force solution (BF), in which each puff individually undergoes the convective propagation and enters the final superposition, is obviously time consuming for a large number of discrete puffs.
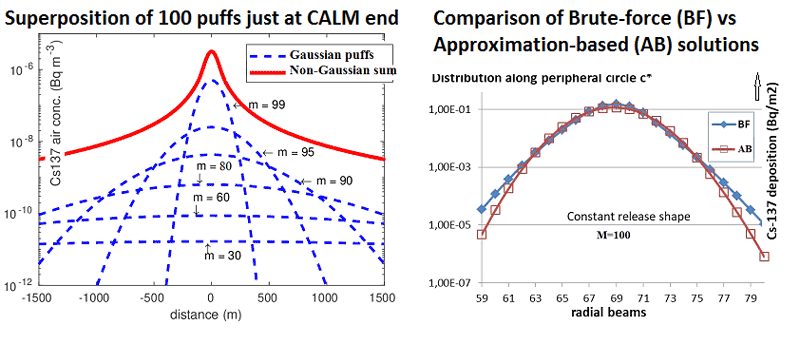
Figure 1 (left): Blue lines: Gaussian distribution of 137Cs concentration in air for a single puff m, each having its own age. Red line: Non-Gaussian distribution of the superposition of all puffs m; m ∈ {1,…,M}.
Figure 2 (right): Comparison of two alternative transport BF and AB (in deposition of 137Cs on the ground around the circle c* - see Figure 3, right).
Simple demonstration example
Let a certain calm episode lasts five hours and immediately after its end the wind begins to blow. The convective transport of the radioactivity clew arises. We trace the drifting over the terrain in the next four hours. Coincidental rain in the fourth hour of the convective transport can cause potentially dangerous increase of the deposited activity of 137Cs (red “patch” in Figure 3- Right).
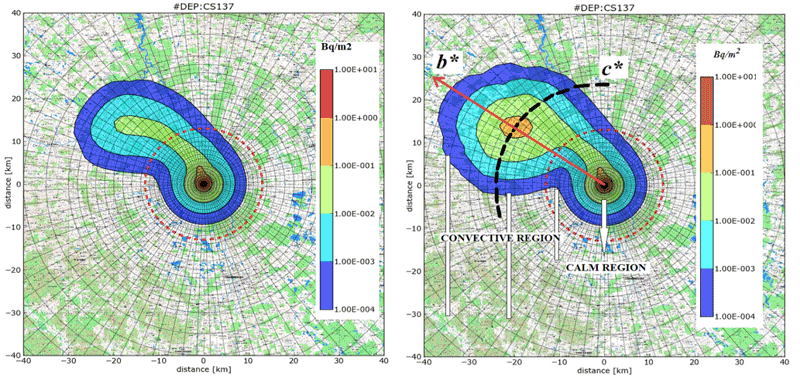
Figure 3: Deposition of radionuclide 137Cs on terrain. M=100, BF solution, the situation just after 9 hours (5 hours of the calm plus 4 hours of the convective transport) from the beginning of the calm. Left: Without atmospheric precipitation. Right: The atmospheric precipitation 1.0 mm.h-1 in the fourth hour of the convective transport causes the serious increase of the deposited activity of 137Cs.
Conclusion
Designed software offers a powerful tool for probabilistic analysis of consequences of the worst-case CALM scenario. The main contribution to methodology lies in proposing the novel approximation-based solution AB, its implementation and tests of its sufficient accuracy. It favourably affects three important areas:
a) AB approach provides comprehensible initial condition for the ensuing convective propagation in the form of optimal Gaussian approximant. The whole “super-puff” clue of radioactivity runs through the convective path only once. It opens way for potential applications of the authentic advanced dispersion codes.
b) Feasibility of prospective computationally intensive Bayesian methods of data assimilation. It has allowed the analysis exploiting the sampling-based procedure requiring a very high number of random samples.
c) Capability to perform the uncertainty and sensitivity analyses [3], forming a suitable base for advanced probabilistic consequence assessment. This probabilistic approach provides the essential data for the desirable transition from a deterministic procedure of the consequence assessment to the probabilistic approach, which enables generation of more informative probabilistic answers to assessment questions.
Links:
[L1] https://www.utia.cas.cz/
[L2] https://havarrp.utia.cas.cz/harp
References:
[1] P. Pecha, et al.: “Determination of Radiological Background Fields Designated for Inverse Modelling”, J. of Atmospheric Environment, 246, 2021, 118105, 2020.
http://library.utia.cas.cz/separaty/2021/AS/pecha-0537537.pdf
[2] M. Kárný M and P. Pecha: “Novel Simulation Technique of Harmful Aerosol Substances Propagation into the Motionless Atmosphere”, Annals of Nuclear Energy, 165, 2021.
https://doi.org/10.1016/j.anucene.2021.108686
[3] P. Pecha and M. Kárný: “A new methodology is outlined and demonstrated on the improvement of uncertainty and sensitivity”, Stochastic Environmental Research and Risk Assessment, 2021. https://doi.org/10.1007/s00477-021-02110-0
Please contact:
Petr Pecha, Institute of Information Theory and
Automation, Czech Republic











