by Balázs Pejó, Gergely Biczók and Gergely Ács (Budapest University of Technology and Economics)
How vital is each participant’s contribution to a collaboratively trained machine learning model? This is a challenging question to answer, especially if the learning is carried out in a privacy-preserving manner with the aim of concealing individual actions.
Federated learning
Federated learning [1] enables parties to collaboratively build a machine learning model without explicitly sharing the underlying, potentially confidential training data. For example, millions of mobile devices can build an accurate input prediction system together without sharing the sensitive texts typed by the device owners [L1], or several pharmaceutical companies can train a single model to predict the bioactivity of different chemical compounds and proteins for the purpose of drug development without revealing which exact biological targets and chemical compounds they are experimenting with [L2]. Unlike traditional centralised learning, where training data from every participant are pooled to build a single model via a trusted entity, in federated learning, clients exchange only model parameter updates (e.g., gradients). Therefore, these model updates represent all the public knowledge about the private training data of different participants.
Although federated learning inherently mitigates some privacy attacks to an extent, it also introduces additional vulnerabilities stemming from its distributed nature. Some participants, called free-riders, may benefit from the joint model without contributing anything valuable in the training phase. Moreover, malicious (byzantine) participants may intentionally degrade model performance by contributing false data or model parameters, referred to as data/model poisoning. In another scenario, some parties may do so unintentionally by incorrectly pre-processing their own training data.
Contribution scores
Contribution scoring allows parties to measure each other’s usefulness when training collaboratively. If implemented carefully, such an approach can detect free-riders and malicious attackers, which intentionally or by chance would degrade model performance. The Shapley value [2], the only provably fair reward allocation scheme, is a candidate for such a contribution metric. Despite being the only reasonable scoring mechanism, the Shapley value is not broadly implemented: it works by computing on every possible subset of the participants and is therefore too demanding for real use-cases. In a machine learning context, this would render the training process impractical: instead of a single joint model trained by all the participants, every possible subset of participants should train a separate model. This is clearly not feasible when even training a single model requires non-negligible time and computational resources.
Many approximation techniques exist to facilitate Shapley value computation, e.g., via the use of gradients, influence functions, reinforcement learning, and sampling. Despite the wide range of available methods, unfortunately, none of them are compatible with privacy-preserving technologies. Indeed, the goal of privacy protection is quite the opposite of any contribution scoring mechanism: the former aims to hide an individual's contribution while the latter aims to measure it.
Our approach
Secure aggregation [3] (see Figure 1) is a frequently used privacy preservation mechanism within federated learning. It is a lightweight cryptographic protocol that allows anybody to glean the sum of the model updates without the individual contributions, i.e., M1, M2, M3, and M4 are concealed with pairwise noises. Therefore, we can only access the models corresponding to the smallest and largest coalitions, i.e., either no-one or everybody updates the model (corresponding to M0 and M respectively). This is clearly not enough information to compute the contribution of the participants as it contains no individual-level information.
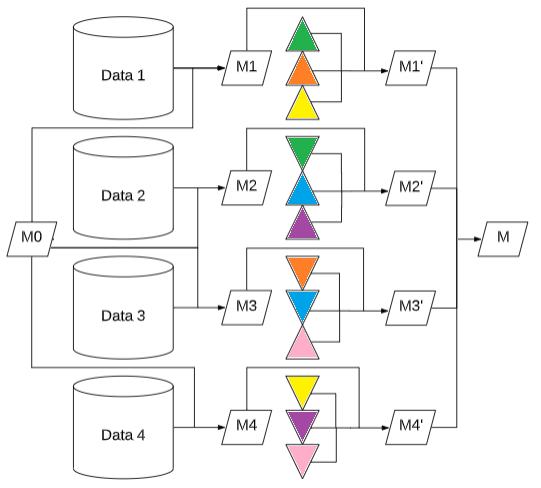
Figure 1: Illustration of Secure Aggregation with 4 parties. M0 is updated by the participants (M1, M2, M3, M4) which are concealed with pairwise noises (M1’, M2’, M3’, M4’) and aggregated into M.
On the other hand, participants do know their own updates as well, hence we can utilise two more coalitions: the one in which they are the only member (i.e., M1, M2, M3, and M4) and the one where they are the only one out (i.e., M-M1, M-M2, M-M3, and M-M4). These latter coalitions form the basis of the Leave-One-Out scoring methods, such as LOO-Stability and LOO-unfairness (e.g., M and M-M1 for participant 1). However, we can obtain a more accurate approximation of a participant’s Shapley value based on four coalitions (e.g., M0, M1, M-M1 and M for participant 1) even if Secure Aggregation is employed (see Figure 1).
Furthermore, since the participants’ data might come from different distributions, they might disagree on contribution scores: a model update assessed as 'good' for someone might be 'bad' for another.
Consequently, based on the participants' evaluations, we might not be able to differentiate between a malicious update and a correct one from a different distribution. Hence, an update originating from a specific distribution should be evaluated on the same distribution, meaning only the participants themselves should evaluate their own updates: this would clearly introduce bias. We can handle this issue in a variety of ways, e.g., consistency can be guaranteed by utilising a smart weighting scheme, or using a public or joint representative dataset for contribution score evaluation on which all participants agree.
Our preliminary results show that our proposed approach is clearly superior to the LOO-based methods, the only other currently existing contribution scoring technique suitable for Secure Aggregation. As future work, we plan to tackle problematic self-reported contributions: the participants might cheat and manipulate their scores. We foresee several solutions to handle this, such as verifiable computation, zero-knowledge proofs, and commitments.
Links:
[L1] https://ai.googleblog.com/2017/04/federated-learning-collaborative.html
[L2] https://www.melloddy.eu/
References:
[1] Q. Yang, et al.: “Federated machine learning: Concept and applications”, ACM Transactions on Intelligent Systems and Technology (TIST) 10.2 (2019): 1-19.
[2] E. Winter: “The shapley value”, Handbook of game theory with economic applications 3 (2002): 2025-2054.
[3] K. Bonawitz, et al.: “Practical secure aggregation for privacy-preserving machine learning”, in proc. of the 2017 ACM SIGSAC Conference on Computer and Communications Security,2017.
Please contact:
Balázs Pejó
CrySyS Lab, HIT, VIK, BME, Hungary











