by Stelios Zimeras (University of the Aegean)
Medical image segmentation is needed for diagnosis and treatment in healthcare. The detection of organs and organic structures in 2D images is an important task during diagnosis. Manual segmentation is very expensive as it requires expertise and is very time consuming. Methods for applying segmentation vary widely depending on the specific application, imaging modality and other factors like treatment (e.g., cancer treatment, image-guided surgery, and invasive techniques) or diagnostic imaging. Therefore, automatic segmentation algorithms are needed [1].
During brain imaging, the segmentation of the organ structure as well as the shape of the tumour is essential for diagnosis and cancer treatment. Figure 1 illustrates a 2D CT brain image where the position of the tumour appears as a shadow.
Image segmentation techniques include methods of regional area identification based on splitting techniques to extract images of structures and provide images that closely represent the real data (2D regions or 3D voxels). Several contour and region approaches to segmentation have been proposed. Contour techniques are often less robust than region techniques and more sensitive to noise and variability of data.
There are three main ways to perform image segmentation: (i) manual: an expert with training draws the required boundaries manually. Manual drawing of boundaries is difficult and time consuming; (ii) fully automatic: the available techniques, such as thresholding or region growing can be applied and they are quite robust for big data medical images; (iii) semiautomated: this method uses boundary finding results generated by sophisticated automatic algorithms as an initial guess.
To reduce the user interaction required for the segmentation, active contour models (ACM) could be introduced, where contours and homogeneous regions are integrated into image structures. ACMs are adaptive contour representations, also known as snakes or deformable models. ACMs are 2D image curves, which are adjusted from an initial approximation to image features by a movement of the curve caused by simulated forces [2]. The idea behind these models is to represent the contours as parts of elasticity and rigidity. The general concept of active contours is autonomous adaptation of the shape and location of objects, finding the important contour points to reconstruct the image. An internal tension of the curve resists against highly angled curvatures, which makes the ACM movement robust against noise. After a starting position is given, it is adapted to an image by relaxation to equilibrium of the external force and internal tension. The method performs a fitting process based on the elasticity of the contour lines. To calculate the forces, an external energy has to be defined. The gradient of this energy is proportional to the external force. ACM models are a class of energy minimising spline curves or surfaces. These models are very important in a number of inverse visual problems such as the segmentation and reconstruction of objects from images in mathematically ill-posed problems [3].
Implementation of the active contour models (ACM) is performed in Figure 2 based on the work of [2]. Based on the resulting images, the tumour’s contour is well defined, with sharp boundaries around the investigating region. The algorithm converges in 100 iterations, performing the optimal results. The performance times are 1.15 seconds for 20 iterations, 1.28 seconds for 50 iterations and 2.32 seconds for 100 iterations.
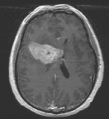
Figure 1: 2D CT brain image: position of the tumour is visible as a shadow.
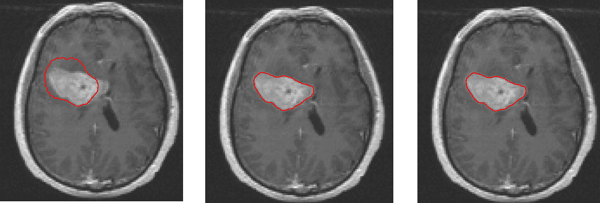
Figure 2: Contour representation of the tumour based on active contour models. From left to right: 20 iterations, 50 iterations, 100 iterations.
References:
[1] S. Zimeras: “Brain segmentation tools under uncertain conditions for radiotherapy treatment planning”, Biomedical Research and Clinical Practice, Vol 4, 1-5, 2019
[2] L. Wang, L. He, A. Mishra, C. Li: “Active contours driven by local Gaussian distribution fitting energy”. Signal Processing, 89 (2009) 2435–2447.
[4] S. Zimeras, G. Karangelis: “Segmentation of anatomical structures using volume definition tools”, Lecture Notes in Computer Sciences 27, Computer Application in Modern Medicine, M., Springer-Verlag, 825-836, 2008.
Please contact:
Stelios Zimeras
University of the Aegean, Greece











