by Alessia Amelio (Univ. of Calabria)
The similarity between images can be computed using a new method that compares image patches where a portion of pixels is omitted at regular intervals. The method is accurate and reduces execution time relative to conventional methods.
To date, researchers have not quite solved the problem of automatically computing the similarity between two images. This is mainly due to the difficulty of filling in the gap between the human visual similarity and the similarity which is captured by the machine. In fact, it requires two important objectives to be fullfilled: (i) to find a reliable and accurate image descriptor that can capture the most important image characteristics, and (ii) to use a robust measure to evaluate similarity between the two images according to their descriptors. Usually a trade-off is needed between these two objectives and the execution time on the machine. An important challenge, therefore, is to achieve computation of an accurate descriptor and a robust measure whilst reducing execution time.
In this paper, I present a new measure for computing the similarity between two images which is based on the comparison of image patches where a portion of pixels is omitted at regular intervals. This measure is called Approximate Average Common Submatrix (A-ACSM) [1] and it is an extension of the Average Common Submatrix (ACSM) measure [2]. The advantage of this similarity measure is that it does not need to extract complex descriptors from the images to be used for the comparison. On the contrary, an image is considered as a matrix, and the similarity is evaluated by measuring the average area of the largest sub-matrices which the two images have in common. The principle underlying this evaluation is that two images can be considered as similar if they share large patches representing image patterns. Two patches are considered as identical if they match in a portion of the pixels which are extracted at regular intervals along the rows and columns of the patches. Hence, the measure is an easy match between a portion of the pixels. This concept introduces an approximation, which is based on the “naive” consideration that two images do not need to exactly match in the intensity of every pixel to be considered as similar. This approximation makes the similarity measure more robust to noise, i.e., small variations in the pixels’ intensity due to errors in image generation, and considerably reduces its execution time when it is applied on large images, because a portion of the pixels does not need to be checked. Figure 1 shows a sample of match between two image patches with an interval of two along the columns and one along the rows of the patches.
Figure 2 depicts the algorithm for computing the A-ACSM similarity measure.
Figure 3 shows how to find the largest square sub-matrix at a sample position (5,3) of the first image.
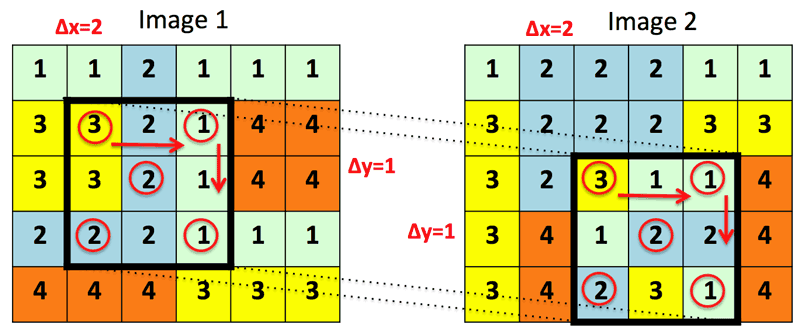
Figure 1: A demonstration sample of match between two patches belonging to images 1 and 2. Each image has four colours which are also numbered from 1 to 4. An interval of Δx=2 and Δy=1 is set respectively along the columns and rows of the patches. Accordingly, the match is only verified between the elements in the red circles. The elements are selected as in a chessboard. In this case, the two image patches perfectly match because all the elements in the red circles correspond to one another.
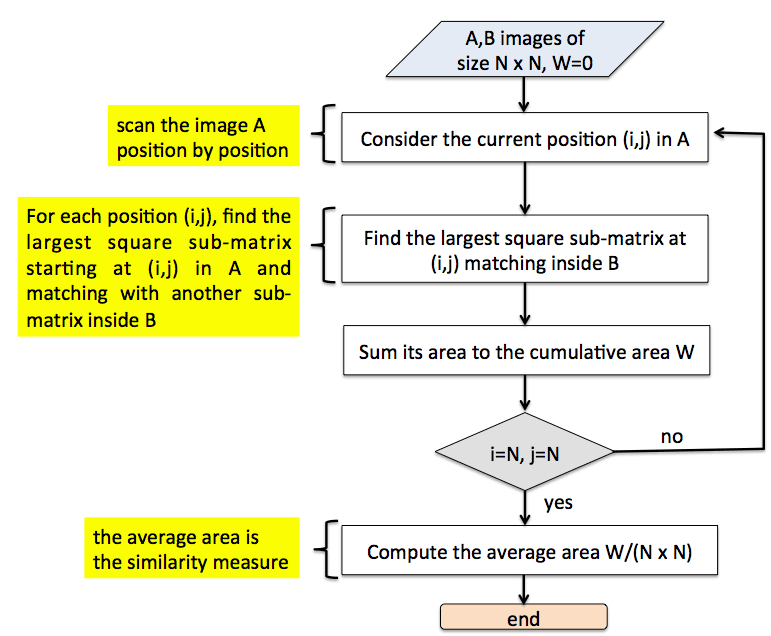
Figure 2: Flowchart of the A-ACSM algorithm.
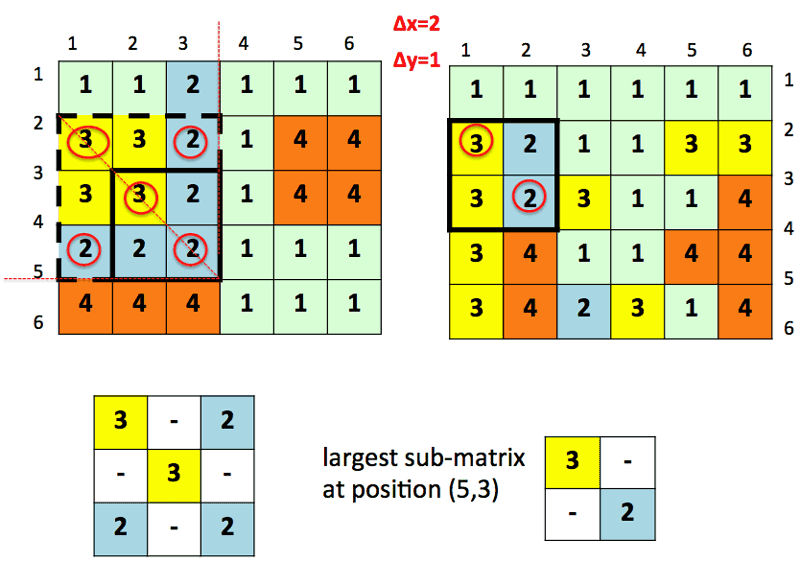
Figure 3: The largest square sub-matrix at position (5,3) of the first image. All the sub-matrices of different size along the main diagonal at (5,3) are considered to match inside the second image. In this case, the sub-matrix of size 3 has no match inside the second image. Hence, the sub-matrix of size 2 is considered. Because it has a correspondence at position (3,2) in the second image, it is the largest square sub-matrix at position (5,3).
The A-ACSM similarity measure, as well as its corresponding dissimilarity measure, has been extensively tested on benchmark image databases and compared with the ACSM measure and other well-known measures in terms of accuracy and execution time. Results demonstrated that A-ACSM outperformed its competitors, obtaining higher accuracy in a lower execution time.
The project of the average common submatrix measures is in its early stage at the Georgia Institute of Technology, USA, and is currently in progress at DIMES University of Calabria, Italy. Future work will extend the submatrix similarity measures with new features and will evaluate the similarity on different types of data, including documents, sensor data, and satellite images [3]. The recent developments in this direction are in collaboration with the Technical Faculty in Bor, University of Belgrade, Serbia.
References:
[1 A. Amelio: “Approximate Matching in ACSM dissimilarity measure”, Procedia Computer Science 96: 1479-1488, 2016.
[2] A. Amelio, C. Pizzuti: “A patch-based measure for image dissimilarity”, Neurocomputing 171:362-378, 2016.
[3] A. Amelio, D. Brodić: The ε-Average Common Submatrix: Approximate Searching in a Restricted Neighborhood, IWCIA: 7-11, (short comm.) arXiv:1706.06026, 2017.
Please contact:
Alessia Amelio, DIMES University of Calabria, Italy











