by Dave Raggett (W3C/ERCIM)
Introduction
Machine reasoning has had little attention over the last decade when compared to knowledge graphs and deep learning. Application logic is usually buried in the program code, making it cumbersome and costly to update. Approaches based upon traditional logic fail to cope with everyday knowledge that inevitably includes uncertainty, incompleteness and inconsistencies, whilst statistical approaches are often impractical given difficulties in obtaining the required statistics.
Plausible reasoning, by contrast, seeks to mimic human argumentation in terms of developing arguments for and against a given premise, using a combination of symbolic statements and qualitative metadata. Let’s start by considering what is meant by knowledge, and its relationship to information and data. Data is essentially a collection of values, such as numbers, text strings and truth values. Information is structured labelled data, such as column names for tabular data. Knowledge is understanding how to reason with information. Knowledge presumes reasoning and without it is just information. As such, it makes sense to focus on automated reasoning for human-machine cooperative work that boosts productivity and compensates for skill shortages.
Business software is for the most part based on relational databases that represent data in terms of tables. There is growing interest in the greater flexibility of graph databases using RDF or Property Graphs. The next stage is likely to see the emergence of cognitive databases featuring human-like reasoning along with support for natural language interaction and multimedia rendering (Figure 1).
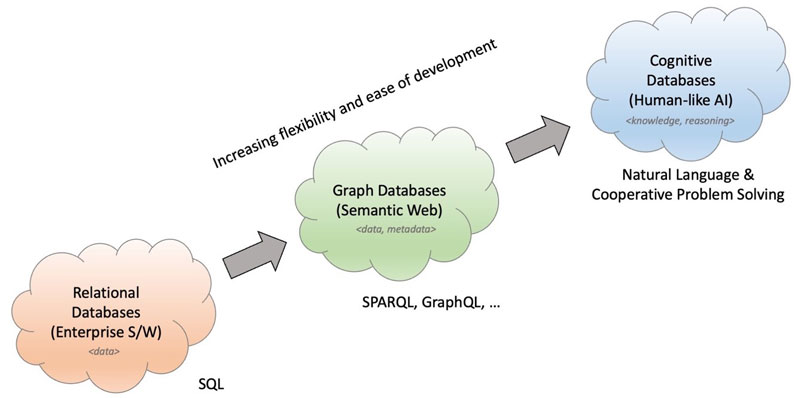
Figure 1: From relational to cognitive databases.
Plausible Reasoning
People have studied the principles of plausible arguments since the days of Ancient Greece, e.g., Carneades and his guidelines for effective argumentation. There has been a long line of philosophers working on this since then, including Locke, Bentham, Wigmore, Keynes, Wittgenstein, Pollock and many others.
Plausible reasoning is everyday reasoning, and the basis for legal, ethical and business decisions. Researchers in the 20th century were side-tracked by the seductive purity of mathematical logic, and more recently, by the amazing magic of deep learning. It is now time to exploit human-like plausible reasoning with imprecise and imperfect knowledge for human-machine cooperative work using distributed knowledge graphs. This will enable computers to analyse, explain, justify, expand upon and argue in human-like ways.
In the real world, knowledge is distributed and imperfect. We are learning all the time, and revising our beliefs and understanding as we interact with others. Imperfect is used here in the sense of uncertain, incomplete and inconsistent. Conventional logic fails to cope with this challenge, and the same is true for statistical approaches, e.g., Bayesian inference, due to difficulties with gathering the required statistics. Evolution has equipped humans with the means to deal with this, though not everyone is rational, and some people lack sound judgement. Moreover, all of us are subject to various kinds of cognitive biases, as highlighted by Daniel Kahneman.
Consider the logical implication A ⇒ B. This means if A is true then B is true. If A is false then B may be true or false. If B is true, we still can't be sure that A is true, but if B is false then A must be false. Now consider a more concrete example: if it is raining then it is cloudy. This can be used in both directions: Rain is more likely if it is cloudy, likewise, if it is not raining, then it might be sunny, so it is less likely that it is cloudy, which makes use of our rough knowledge of weather patterns.
In essence, plausible reasoning draws upon prior knowledge as well as on the role of analogies, and consideration of examples, including precedents. Mathematical proof is replaced by reasonable arguments, both for and against a premise, along with how these arguments are to be assessed. In court cases, arguments are laid out by the Prosecution and the Defence, the Judge decides which evidence is admissible, and the guilt is assessed by the Jury.
During the 1980’s Alan Collins and co-workers developed a core theory of plausible reasoning based upon recordings of how people reasoned aloud [R1]. They discovered that:
- There are several categories of inference rules that people commonly use to answer questions.
- People weigh the evidence bearing on a question, both for and against, rather like in court proceedings.
- People are more or less certain depending on the certainty of the premises, the certainty of the inferences, and whether different inferences lead to the same or opposite conclusions.
- Facing a question for which there is an absence of directly applicable knowledge, people search for other knowledge that could help given potential inferences.
A convenient way to express such knowledge is the Plausible Knowledge Notation (PKN). This is at a higher level than RDF, and combines symbols with sub-symbolic qualitative metadata. PKN statements include properties, relationships, dependencies and implications. Statements may provide qualitative parameters as a comma separated list in round brackets at the end of the statement.
Qualitative metadata is used to compute the degree of certainty for each inference, starting from the certainty of the known facts, and using algorithms to combine multiple sources of evidence:
- typicality in respect to other group members, e.g., robins are typical song birds;
- similarity to peers, e.g., having a similar climate;
- strength, inverse – conditional likelihood in each direction, e.g., strength of climate for determining which kinds of plants grow well;
- frequency – proportion of children with given property, e.g., most species of birds can fly;
- dominance – relative importance in a given group, e.g., size of a country’s economy;
- multiplicity – number of items in a given range, e.g., how many different kinds of flowers grow in England.
How does this support reasoning? Let’s start with something we want to find evidence for
flowers of England includes daffodils
and evidence against it using its inverse:
flowers of England excludes daffodils
We first check if this is a known fact and if not look for other ways to gather evidence.
We can generalise the property value:
flowers of England includes ?flower
We find a matching property statement:
flowers of England includes temperate-flowers
We then look for ways to relate daffodils to temperate flowers:
daffodils kind-of temperate-flowers
Allowing us to infer that daffodils grow in England.
Alternatively, we can generalise the property argument:
flowers of ?place includes daffodils
We look for ways to relate England to a similar country:
Netherlands similar-to England for flowers
We then find a related property statement:
flowers of Netherlands includes daffodils, tulips.
This also allows us to infer that daffodils grow in England. The certainty depends on the parameters, in this case “similarity”. These examples use properties and relationships, but we can also look for implications and dependencies, e.g., a medium latitude implies a temperate climate, which in turn implies temperate flowers. We can prioritise inferences that seem more certain, and ignore those that are too weak.
A proof-of-concept web-based demo can be found in [L1]. It introduces the plausible knowledge notation and applies it to a suite of example queries against a cognitive knowledge base, including reasoning by analogy and the use of fuzzy quantifiers, something that is needed to support the flexibility of natural language, e.g., none, few, some, many, most and all, as in:
Are all English roses red or white?
all ?x where colour of ?x includes red, white from ?x kind-of rose and flowers of England includes ?x
Are only a few roses yellow?
few ?x where colour of ?x includes yellow from ?x kind-of rose
Which English roses are yellow?
which ?x where colour of ?x includes yellow from ?x kind-of rose and flowers of England includes ?x
Are most people older than 20?
most ?x where age of ?x greater-than 20 from ?x isa person
Is anyone here younger than 15?
any ?x where age of ?x less-than 15 from ?x isa person
How many people are slightly younger than 15?
count ?x where ?x isa person and age of ?x slightly:younger-than 15
How many people are very old?
count ?x where ?x isa person and age of ?x includes very:old.
Plausible reasoning embraces Zadeh’s fuzzy logic in which scalar ranges are described as blend of overlapping values for imprecise concepts like warm and cool. This enables simple control rules to be expressed using terms from the ranges. Fuzzy sets correspond to multiple lines of argument, e.g., the certainty that the fan speed is stopped, slow or fast. Fuzzy modifiers model adverbs and adjectives, such as very, slightly and smaller, by transforming how terms relate to scalar ranges.
Analogical queries can be solved by looking for structural similarities, e.g.,
| leaf:tree::petal:? | short:light::heavy:? |
|
leaf part-of tree petal part-of flower |
short less-than long for size light less-than heavy for weight |
When comes to scaling to very large knowledge graphs, an attractive approach is to decompose large graphs into overlapping smaller graphs that model individual contexts. Such contexts are needed to support reasoning about past, present and imagined situations, e.g., when reasoning about the future or counterfactual reasoning about causal explanations. Contexts are also needed for natural language, e.g., consider “John opened the bottle and poured the wine”. This is likely to be a social occasion with wine being transferred to the guests’ glasses, with a context associated with causal knowledge, e.g., to pour liquid from a closed bottle, it first needs to be opened.
Humans find coherent explanations very quickly when listening to someone speaking. One potential mechanism to mimic this is to exploit spreading activation. This can be used to identify shared contexts and the most plausible word senses, as well as to mimic characteristics of human memory such as the forgetting curve and spacing effect. Spreading activation can also be applied to guide search for potential inferences as part of the reasoning process, as noted by Collins.
The web-based demo [L1] uses a small set of static reasoning strategies. Further work is needed to introduce metacognition for greater flexibility, and to reflect the distinction between System 1 & 2 thinking as popularised by Daniel Kahneman in his work on cognitive biases. Work is now underway to demonstrate how short natural language narratives can be understood using plausible reasoning over common sense knowledge, along with the role of metaphors and similes.
This can be contrasted with large language models derived using deep learning in that the latter rely on statistical regularities using opaque representations of knowledge that aren’t open to inspection. The ability to explain and justify premises is a clear benefit of plausible reasoning. An open question is how to integrate plausible reasoning with approaches based upon deep learning, e.g. for applying everyday knowledge to improve overall semantic consistency for images generated from text prompts.
A further challenge will be to support continuous learning, e.g., syntagmatic learning about co-occurrence regularities, paradigmatic learning about abstractions, and skill compilation for speeding common reasoning tasks. Learning can be accelerated through the use of cognitive databases shared across many cognitive agents as a form of artificial hive mind, and combined with knowledge derived from large corpora.
This work has been supported through funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 957406 (TERMINET) and No. 833955 (SDN-microSENSE).
Link:
[L1] A web-based proof of concept: https://www.w3.org/Data/demos/chunks/reasoning/
Reference:
[1] The Logic of Plausible Reasoning: A Core Theory: Allan Collins & Ryszard Michalski, Cognitive Science 13, (1):1-49 (1989).
Please contact:
Dave Ragett, W3C/ERCIM,











