by Balázs Pejó (Budapest University of Technology and Economics) and Delio Jaramillo Velez (Chalmers University of Technology)
To what extent do individual contributions enhance the overall outcome of collaborative work? This question naturally arises across scientific fields and is particularly challenging in Federated Learning. It remains largely unexplored in privacy-preserving settings where individual actions are concealed with techniques like Secure Aggregation.
Federated Learning (FL) [1] enables multiple parties to develop a machine learning model collaboratively without sharing their confidential training data. For instance, millions of mobile devices can collectively train a predictive text model without exposing their personal texts, or multiple hospitals can jointly train a model to predict various health-related risk scores without revealing specific patients’ sensitive medical records. Unlike centralized learning, where the training data from all participants are collected by a trusted entity, FL only involves the exchange of model parameter updates.
As such, FL comes with some built-in privacy protection. Yet, information could still leak through the model updates, which require additional techniques to reduce the privacy risk. Secure Aggregation (SA) [2] is a frequently used privacy-preserving mechanism that hides individual model updates via a lightweight cryptographic protocol. On the other hand, advanced privacy protection, such as SA, also helps malicious parties to remain undetected within the federation. For instance, adversarial (Byzantine) participants can degrade model performance stealthily through (data of model) data poisoning attacks due to the utilized privacy-enhancing technology (PET). Moreover, unintentional manipulations can even occur, such as when participants have biased or noisy training data they are unaware of.
To tackle these issues, the usefulness of individuals should be determined. Contribution Evaluation (CE) schemes allow participants to assess each other’s value, thus, helping to identify potential harmful actors that could degrade the model’s performance. The Shapley value (SV) [3] is a prominent candidate for CE, as it considers the marginal contributions of the participant to all possible coalitions. However, the SV is computationally demanding, thus, it is not feasible for large models or big datasets. Consequently, numerous approximation methods exist to relax its computational demands. On the other hand, they also rely on marginal contributions, which is incompatible with PETs such as SA. Indeed, there is a fundamental tension between them: privacy, in general, aims to conceal individual-specific information, while CE, conversely, seeks to obtain the individual’s usefulness (e.g., measured in data quality).
A possible solution to this problem was envisioned in [4], where the marginal contributions based on the coalitions with the two extreme cardinalities are considered. These are the grand coalition (when everybody trains, i.e., the output of SA) and the empty coalition (when no one trains, i.e., the untrained model). These can be combined with individual coalitions, which are available to the participants but not to others due to SA.
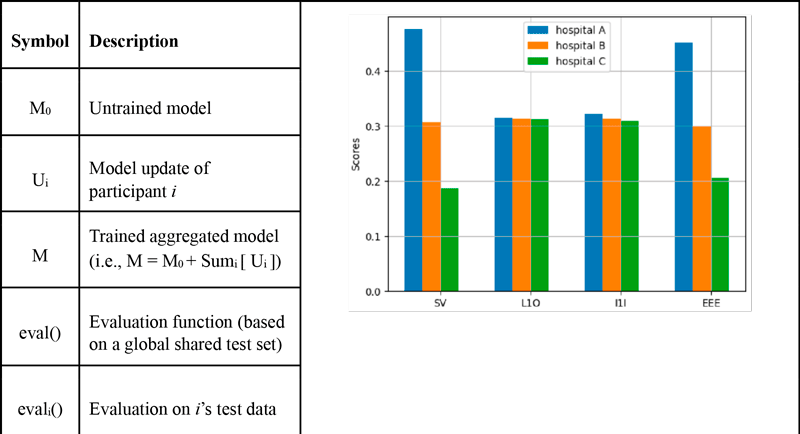
Figure 1: CE scores for three FL clients. The model is logistic regression, the dataset is Breast Cancer Wisconsin with added Gaussian noises: σ is 0.1, 0.3, and 0.5 for the clients, respectively.
Following the notation in Table 1, these scores are denoted as Include-One-In (I1I) and Leave-One-Out (L1O) and computed as follows for the ith participant:
I1Ii = eval ( M0 + Ui ) - eval ( M0 )
L1Oi = eval ( M ) - eval ( M - Ui )
A shortcoming of this approach is the centralized nature of the evaluation: the marginal contributions for I1I and L1O are based on individual local updates, but they are measured via a global, pre-agreed test set. In reality, the participants’ data might come from different distributions, hence, inconsistencies might arise, like disagreements on contribution scores: a model assessed as ‘good’ for someone might be ‘bad’ from another’s point of view. Therefore, one’s contribution should not be determined by themselves, as that would lead to misaligned incentives and introduce bias into the assessment. Instead, the participants should be evaluated by everybody else.
Our proposed scoring algorithm is called Evaluate-Everyone-Else (EEE), as all participants evaluate each other except themselves. More precisely, they evaluate the others together as one instead of individually, which is prevented by SA. Formally, EEE for participant i is the sum of all the marginal contributions of everybody else from all participants’ points of view, as shown below.
EEEj = Sumi≠j [ evali ( M ) - evali ( M0 + Ui ) ]
For example, if there are three hospitals (named A, B, and C) performing FL together with SA, the EEE score of A can be evaluated by B and C as follows:
● EEEA = [ evalB ( M ) - evalB ( M0 + UB ) ] + [ evalC ( M ) - evalC ( M0 + UC ) ]
● EEEA = [evalB (M0 + UA + UB + UC) - evalB (M0 + UB)] + [evalC (M0 + UA + UB + UC) - evalC (M0 + UC)]
● EEEA = [Marginal cont. of {A,C} according to B]+[Marginal cont. of {A,B} according to C]
Thus, the EEE score for A is the sum of the local views of B and C about everybody else. Although this score encompasses others’ contributions explicitly, they are counted fewer times as the participant score is assigned to: EEEA is influenced by {A,C} and {A,B}, so the impact of B and C are also included, their influence is less than that of the target A. To visualize the exact values for the envisioned scenario, we split a medical dataset into three (assigned to A, B, and C) and artificially injected different amounts of noise into them. In Figure 1, we show the baseline SV, the privacy-preserving self-evaluation methods I1I and L1O, and the proposed (both privacy- and incentive-aware) EEE. It is visible that our approach approximates the ground truth SV much better.
Our proposed technique is the first privacy-friendly contribution evaluation technique that mitigates the rising selfish incentives concerning self-evaluation. Furthermore, the evaluation is completely distributed as it does not require any common representative dataset of the participants for a coherent evaluation.
References:
[1] P. Kairouz, et al., “Advances and open problems in federated learning”. Foundations and trends in machine learning, 2021.
[2] M. Mansouri, et al., “Sok: SA based on cryptographic schemes for FL”. Proceedings on Privacy Enhancing Technologies, 2023.
[3] A. E. Roth, “The Shapley Value: Essays in honor of Lloyd S. Shapley”. Cambridge University Press, 1988.
[4] B. Pejó, et al., “Measuring contributions in privacy-preserving federated learning”. ERCIM News 126, 2021
Please contact:
Balázs Pejó
CrySyS Lab, HIT, VIK, BME, Hungary











