by Loizos Michael (Open University of Cyprus & CYENS Center of Excellence)
AI systems that are compatible with human cognition will not come as an afterthought by patching up opaque models with post-hoc explainability. This article reports on our research program to develop Machine Coaching, a computationally efficient and cognitively light paradigm that supports a form of interactive and developmental machine learning, through supervision that is not only functional, on “what” decisions should be made, but also structural, on “how” they should be made. We discuss the role that this paradigm can play in neural-symbolic systems, in operationalizing fast intuitive and slow deliberative thinking, and in supporting the explainability and contestability of AI systems by design.
A salient characteristic of data-driven neural-based approaches to machine learning is the autonomous identification of intermediate-level concepts, which then serve to scaffold higher-level decisions. These identified concepts do not necessarily align with familiar human concepts, which leads to a perception of opaqueness of the learned models. Post-hoc explainability methods can serve only in explicating the intermediate-level concepts in a learned model, but not in addressing the misalignment problem.
The problem is manifest in learning settings where the empirical generalizations leading to intermediate-level concepts are not directly pitted against a ground truth. Tackling misalignment requires, therefore, a non-trivial human-machine collaboration [1], during which a learner and a coach — who could be the learner’s parent, teacher, or senior colleague in the case of a human learner, and a domain expert, or a casual user of the learned model in the case of a machine learner — engage in a dialectical and bilateral exchange of explanations of whether and how a decision should relate to intermediate-level concepts.
A coaching round begins when the learner faces a situation that calls for the making of a decision using the current learned model. Regardless of the decision’s functional validity (i.e., whether the decision is correct), the coach can inquire for evidence of the decision’s structural validity (i.e., whether the reasons for making that decision are correct). Upon receiving such a query, the learner returns arguments that decompose the decision as a simple function (e.g., a short conjunction) of intermediate-level concepts. Further inquiries can prompt the learner to decompose those concepts to even lower-level concepts. If the coach identifies an argument to be missing or unacceptable, the coach can offer a counterargument of how the decomposition could have been done better. The round concludes with the learner integrating the counterargument into the learned model, giving it preference over all existing conflicting arguments, and adopting it as part of the learner’s pool of arguments that are available for use in subsequent rounds.
It can be formally shown that the process converges, in a computationally efficient manner, to a learned model that is, with high probability, structurally (and functionally) valid in a large fraction of all future situations [2]. The resulting structural validity entails the alignment of the learned model’s intermediate-level concepts with those of the coach, while the rich interactive feedback enhances learnability beyond that of standard supervised learning. Concept alignment and enhanced learnability come with minimal extra burden for the coach, as suggested by evidence from Cognitive Psychology that argumentation is inherent in human reasoning, and that the offering of counterarguments is cognitively light. Relatedly, the coach’s counterarguments are not required to be optimal, but merely satisficing in a given situation.
Depending on the nature of the application domain, the online engagement of the coach can be alleviated by alternating between a deployment phase, where the learned model makes multiple decisions, and a development phase, where the coach examines the functional and structural validity of a selected subset of those decisions. In domains where the functional validity (and perhaps the criticality) of decisions can be ascertained objectively, a certain number of incorrect (critical) decisions could trigger the transition to the development phase, where only those decisions will be further probed for their structural validity.
Nothing restricts the learned model to being purely symbolic, nor the irreducible concepts, reached by the iterated decomposition of intermediate-level concepts, to being directly observable. Instead, irreducible concepts can act as an interface between a neural and a coachable module in the learned model. Neural-symbolic techniques can be used to train the neural module so that its outputs seamlessly feed into the coachable module, and so that the latter module’s arguments provide supervision signals for the former [3]. The development phase can be extended to include a neural training round after each coaching round. The structure of the learned model is shown in Figure 1.
According to this structured learned model, each potential decision with respect to some concept has an explanation that comes from direct neural perception. Decisions that structurally employ this first type of explanation resemble those coming from the fast and intuitive (System 1) thinking process of the human mind. For some concepts (namely, the reducible ones), there exist additional explanations that come from associative symbolic inferencing. Decisions that structurally employ this second type of explanation resemble those coming from the slow and deliberative (System 2) thinking process of the human mind. The argumentative nature of the learned model offers, then, an operationalization of the System 1 versus System 2 distinction as a difference in the effort put into determining the acceptability of arguments in the symbolic module of the learned model. With minimal effort, the argument “predict the neural module percept” is accepted uncontested, while extra effort allows the consideration of additional arguments that may defeat the former one, and lead to the making of possibly distinct decisions.
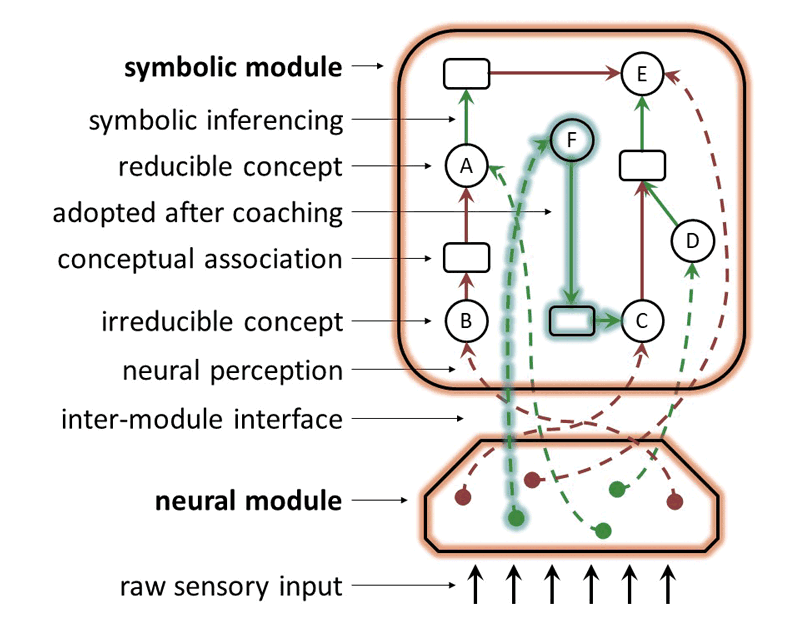
Figure 1: Depiction of a learned model with a neural-symbolic structure. The learned model receives raw sensory inputs through its neural module, maps them into a vector of output values, and maps each output value to one of the concepts in the symbolic module in a bijective manner. Reducible concepts in the symbolic module relate to other concepts through conceptual associations, which are viewed as expressing supporting or attacking arguments. Each of the two modules implements three methods: (a) deduction, for returning the output of a module when given a certain input, (b) abduction, for returning potential inputs of the module that give rise to a certain output, and (c) induction, for revising the module’s part of the learned model. Induction for the neural module can utilise standard neural training techniques, while induction for the symbolic module can utilise machine coaching. The learned model as a whole makes decisions and is revised by combining the methods of its two constituent modules.
The argumentative nature of the symbolic module supports the offering of explanations of the learned model’s decisions not only in the standard attributive fashion used in post-hoc explainability, but also in a contrastive fashion against other candidate decisions that rely on defeated arguments. Additionally, the structural validity of the symbolic module allows the learned model to demonstrate, by design, the compliance of its decisions against the coach’s held policy, in case those are contested.
This work was supported by funding from the EU’s Horizon 2020 Research and Innovation Programme under grant agreements no. 739578 and no. 823783, and from the Government of the Republic of Cyprus through the Deputy Ministry of Research, Innovation, and Digital Policy. Additional resources for Machine Coaching, including online services and demonstration scenarios, are available at [L1].
Link:
[L1] https://cognition.ouc.ac.cy/prudens
References:
[1] L. Michael, “Explainability and the Fourth AI Revolution” in Handbook of Research on Artificial Intelligence, Innovation, and Entrepreneurship, Edward Elgar Publishing, 2023. https://arxiv.org/abs/2111.06773
[2] L. Michael, “Machine Coaching”, in Proc. of XAI @ IJCAI, p. 80–86, 2019. https://doi.org/10.5281/zenodo.3931266
[3] E. Tsamoura, T. Hospedales, L. Michael, “Neural-Symbolic Integration: A Compositional Perspective”, in Proc. of AAAI, p. 5051–5060, 2021. https://doi.org/10.1609/aaai.v35i6.16639
Please contact:
Loizos Michael, Open University of Cyprus & CYENS Center of Excellence, Cyprus











