by Gábor Szederkényi (Pázmány Péter Catholic University), Tamás Péni (SZTAKI) and Gergely Röst (University of Szeged)
A control theoretic approach can efficiently support the systematic design of strategies to suppress or mitigate the effects of the COVID-19 pandemic.
The COVID-19 pandemic is one of the biggest challenges the world is currently facing. Until a vaccine and effective treatment are available, carefully planned measures are needed in every country to control the spread of the disease. Choosing the right management policy is a sensitive task that requires several potentially contradicting objectives to be considered. The most important limiting constraint is the capacity of the healthcare system, which can easily be overwhelmed if the spread of the disease is not controlled. It is clear that the transmission of the virus can be efficiently slowed down by appropriate restrictions (social distancing, lockdown), but these measures have negative social and economic impacts that we can’t afford to overlook. At the moment, governments are continuously evaluating their control measures, trying to find a balance between public health concerns and the costs of social distancing measures. This paper shows that control theory provides an appropriate framework for the support of decision-making through the systematic design of optimal management strategies.
A mathematical model of the epidemic spread
The computation of the control policy requires a mathematical model describing the relationship between important time-dependent quantities and capable of predicting the future behaviour of the epidemic. The most common approach is to use compartmental models [1] for this purpose. In this modelling framework the total population is divided into groups (compartments) such that each compartment collects individuals of the same infection status. One possible grouping is obtained by introducing the following compartments [2]: Susceptible (S) collects individuals who can be infected ; Latent (L) contains those who have already contracted the disease, but do not show symptoms and are not infectious yet. Individuals who have just recently been infected and need a few more days to develop symptoms are collected in class Pre-symptomatic (P). Depending on whether or not an infected individual develops symptoms he/she belongs to the compartment Symptomatic infected (I) or Asymptomatic infected (A). Three additional groups are defined for the Hospitalised (H), Recovered (R) and Deceased (D) individuals. The transition diagram representing the interconnections between the compartments is depicted in Figure 1. The transmission rates are given in the labels of the arrows. The model depends on several parameters (α,β,ρ, etc.) which can be determined and continuously updated by following the current literature and analysing the data registered worldwide on the active COVID-19 cases (e.g., L1).
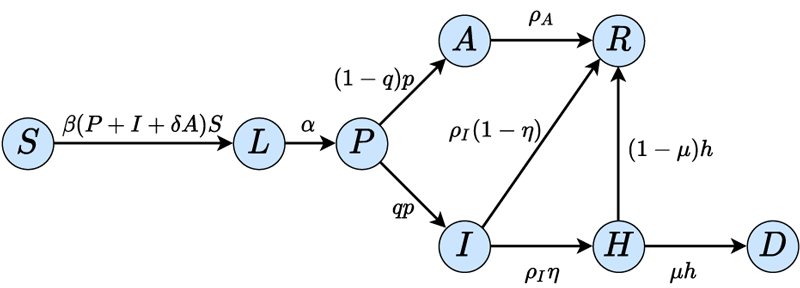
Figure 1: Transition diagram of the compartmental model describing the transmission dynamics of COVID-19.
Formulating COVID management as a control design task
In a control theory framework, dynamical systems are considered as operators mapping from an input signal (function) space to an output space. We distinguish between manipulable inputs which can be set (often between certain limits) by the user and disturbance inputs from the environment that cannot be directly influenced. The outputs are either directly measured quantities or they are computed from measurements. The inner variables representing the actual status of the model are the states. The control goals can be prescribed by defining constraints and optimality criteria for the predicted future behaviour of the system. Possible examples for the former are (physical) bounds on the inputs and/or on the state variables and minimal control costs or operation time for the latter. Therefore, a complex control problem can be expressed in the form of constrained optimisation [2]. In the compartmental model introduced above the control input is the scaling factor of coefficient β determining infection probability. By applying restrictions of varying stringency index (from mandatory mask wearing through closing of different institutions and limiting public gatherings to total lockdown) this factor can be varied between well-defined limits. Assuming that the number of hospitalised and deceased individuals can be reliably documented, these two quantities are chosen for outputs. The main goals of epidemic management, such as protecting the healthcare system and applying less stringent interventions to avoid social and economic crisis, can be formalised by defining a strict upper limit for the number of hospitalised individuals (e.g., H≤Hmax) and adding the control cost to the optimality criteria.
State estimation
In order to use the model to predict the future behaviour of the epidemic, information is needed about the non-measured compartments. The state variables corresponding to these have to be estimated from the past measurements and the applied control actions using the nonlinear compartmental model.
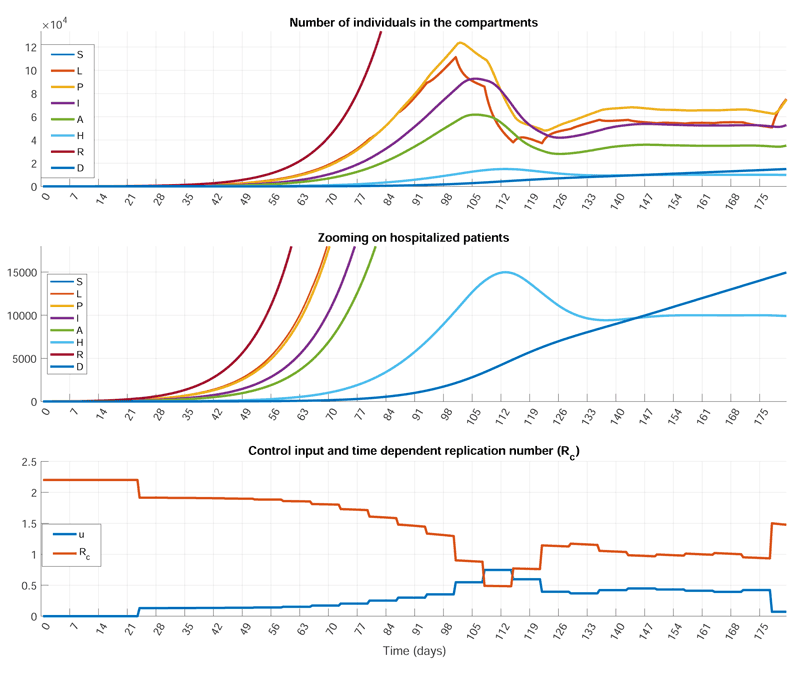
Figure 2: Simulation results obtained by a predictive controller computed by constrained optimisation. The goal is to mitigate the effect of the epidemic and protect the functionality of the healthcare system by taking less stringent measures. The limitation of the healthcare system is modelled by specifying two upper bounds Hmax.(1) and Hmax(2) with Hmax(1) < Hmax(2) for the number of hospitalised patients (H). The primary goal is to keep H under Hmax(1). If this is not possible, this limit can be exceeded, but only up to Hmax(2) and only for a given time period. The control input can vary between “no-interventio”‘ and “total lockdown”‘. It can be seen that the required control goal can be achieved by applying strict measures at the very beginning of the epidemic and systematically easing the restrictions thereafter. Together with the control input, the bottom figure depicts the time dependent replication number (Rc ) as well.
Illustrative results
Figure 2 presents a simulation result obtained by performing the control design concept above for the Hungarian situation. In this specific scenario, we assumed that the capacity of the healthcare system (Hmax) can be temporarily exceeded if needed, but only for a short time and by only a specific amount. This scenario models the actual, real situation, when there is an extra, but limited and possibly costly reserve in the healthcare system that can be activated if necessary.
This research was partially supported by the Artificial Intelligence Hungarian National Laboratory, https://milab.hu/
Links:
[L1] COVID-NET: A weekly summary of US COVID-19 Hospitalization Data: https://gis.cdc.gov/grasp/COVIDNet/COVID19_5.html
References:
[1] S. V. Rakovic, W. S. Levine (editors): “Handbook of Model Predictive Control”, Birkhauser 2019.
[2] F. Brauer, C. Castillo-Chavez, Z. Feng (editors): “Mathematical Models in Epidemiology”, Texts in Applied Mathematics, 69, 1st ed. 2019.
[3] T. Péni, B. Csutak, G. Szederkényi, G. Röst: “Nonlinear model predictive control with logic constraints for COVID-19 management”, Nonlinear Dynamics, 2020.
Please contact:
Tamás Péni
SZTAKI, Hungary











