by Tristan van Leeuwen (Utrecht University), Ajinkya Kadu (Utrecht University) and Wim A. Mulder (Shell Global Solutions International B.V. / Delft University of Technology)
For many decades, seismic studies have been providing useful images of subsurface layers and formations. The need for more accurate characterisation of complex geological structures from increasingly large data volumes requires advanced mathematical techniques and high performance algorithms.
Detailed images of subsurface structures can be obtained by studying the echoes of controlled seismic sources. For many decades, such techniques have been used for engineering purposes, scientific investigations of the Earth’s structure and oil and gas exploration. As the seismic waves travel through the Earth, they are reflected at the interfaces between layers or formations of different rock type. Assuming that the contrast between these structures is small, we can define a linear relationship between the image and the data. Mathematically speaking, this linear transformation enjoys the special property that it preserves singularities. Hence, images of the various interfaces (singularities) can be obtained by applying the transformation in reverse. Techniques based on this linear formalism have been used for many decades and are still the workhorse in many settings.
As opposed to many other sound-based imaging modalities, such as medical ultrasound, the speed of sound in the subsurface can be strongly heterogeneous and is not known a priori. This can be problematic as strong lateral variations of the sound speed cause distortions in the image. Because the data are typically redundant, they enable the generation of multiple, independent images. Imposing consistency between the various images allows one to estimate the spatially varying sound speed. This additional step of estimating the sound speed is specific to seismic imaging but bears some resemblance to calibration problems found in other imaging modalities. An extensive overview is given by [1].
In more complex geological settings, the contrasts between layers is large and we can no longer approximate the image formation process as being linear. A prime example is shown in Figure 1, where a subsurface salt body has a large sound speed and density contrast with the surrounding sediments. Instead of a linear imaging problem, we now have to solve a non-linear parameter estimation problem. This entails repeatedly simulating the seismic experiment with detailed numerical models for wave propagation and updating the parameters until the simulations fit the data. Given its formidable computational burden, current research is aimed at reducing its cost by working on small subsets of the data [2]. Moreover, the number of parameters that need to be estimated is large, even if we assume that the surrounding medium varies smoothly. Because we do not know the salt geometry a priori, we have no choice but to represent the entire medium on a very fine grid. Due to limitations of the aperture, we cannot estimate all these parameters independently. Also, the solution to the non-linear problem is not unique. Figure 2 illustrates the result of a standard parameter estimation technique. Even if we assume the sound speed in the surrounding medium to be known, the reconstruction of the geometry of the salt body is not very accurate.
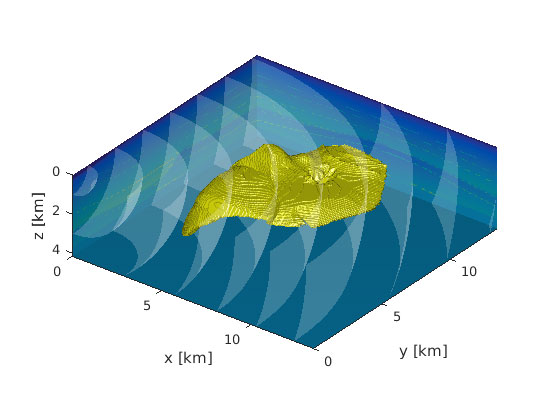
Figure 1: A subsurface salt body is insonified by seismic sources near the Earth’s surface (at z=0). The goal is to retrieve the geometry of the salt body and the surrounding medium from recordings of the response at the Earth’s surface.
To reduce the number of parameters, we split the problem in two parts: a geometric inverse problem for the salt body and a parameter-estimation problem for the surrounding medium. The geometric inverse problem is formulated with a level-set function [3]. The salt geometry is now implicitly defined as the zero contour of this level-set function. Assuming that both the level-set function and the surrounding medium are smooth, we can efficiently represent them with relatively few degrees of freedom. The result of this joint approach is shown in Figure 3. Here, we parametrized the level-set function with radial basis functions and assumed the sound speed in the surrounding medium to be linearly increasing with depth. The resulting number of unknown parameters in the level-set approach is 5x102 as compared to 12x103 in the conventional method. The level-set function and the surrounding medium are estimated in an alternating fashion.
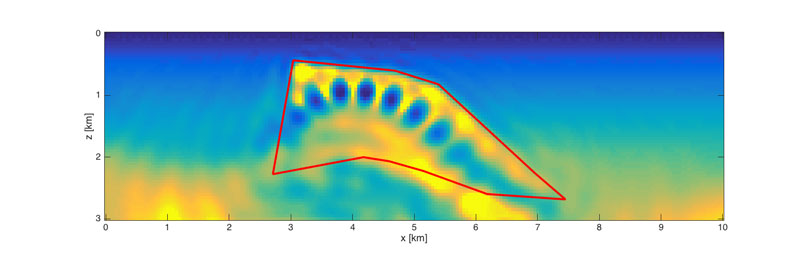
Figure 2: Reconstructed parameters using a conventional method. The true salt geometry (indicated in red) is not well recovered and spurious structure is introduced in the surrounding area.
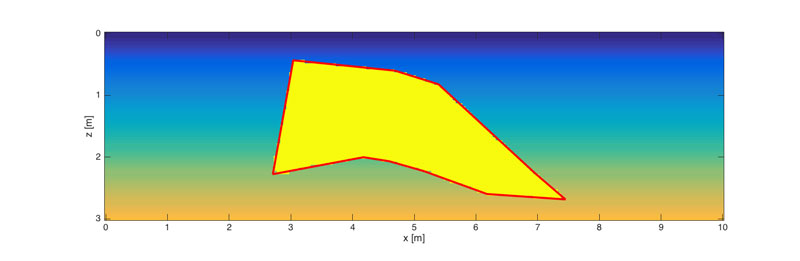
Figure 3: Reconstructed salt geometry and parameters using a level-set method. The true salt geometry (indicated in red) is recovered almost perfectly.
In summary, seismic imaging in the presence of salt bodies can be split into a geometric inverse problem for the salt body and a parameter-estimation problem for the surrounding medium. This separation greatly reduces the number of parameters that need to be estimated and leads to improved reconstructions.
This project is part the Computational Science for Energy Research programme jointly funded by the Foundation for Fundamental Research on Matter (FOM), the Netherlands Organization for Scientific Research (NWO), and Shell.
References:
[1] W.W. Symes: “The seismic reflection inverse problem”, Inverse Problems, 25 (12), 123008, 2009
[2] T. van Leeuwen, F. J. Herrmann: “3D Frequency-Domain Seismic Inversion with Controlled Sloppiness”, SIAM Journal on Scientific Computing, 36(5), 192–217, 2014.
[3] A. Aghasi, M. Kilmer, E. L. Miller: “Parametric Level Set Methods for Inverse Problems”, SIAM Journal on Imaging Sciences, 4(2), 618–650, 2011.
Please contact:
Tristan van Leeuwen
Utrecht University, the Netherlands











