by Arthur Mensch, Julien Mairal, Bertrand Thirion and Gaël Varoquaux (Inria)
A new algorithm developed at Inria gives large speedups for factorise matrices that are huge in both directions, a growing need in signal processing. Indeed, larger datasets are acquired every day, with more samples of richer signals. To capture interpretable latent representations in these very big data, matrix factorisation is a central tool. But such decompositions of terabytes of data come with a hefty cost.
New generation data acquisition gives rise to increasingly high dimensional signals: higher resolution in new sensors or better tracking on internet infrastructures. As the overall number of data points collected also increases, the resulting data are huge in both sample and feature size. For instance in brain imaging, new scanners yield images that typically comprise a million voxels. They are used for population imaging, acquiring thousands of time-resolved images for thousands of subjects. In e-commerce, the classic Netflix movie-recommendation dataset comprises more than 100 million ratings. As these datasets are large in both directions, latent factors are often used to capture a lower-dimensional structure. Matrix factorisation is a good solution, often framed as sparse dictionary learning. However, the size of the data poses a severe computational problem. Indeed, for matrices large in only one direction, stochastic optimisation is an efficient solution, for instance online dictionary learning on many measurements of small signals. To tackle efficiently large dimensionality in such online settings, we introduced random subsampling in the stochastic optimisation [1]. The resulting subsampled online algorithm gives up to 10-fold speedups compared to the state-of-the-art online dictionary learning algorithm in brain imaging or movie-recommendation settings.
State of the art: online dictionary learning
The online dictionary learning of Mairal 2010 [2] represents the state of the art in settings with many samples. Using a sparse dictionary-learning formulation, it tackles matrix factorisation by learning a dictionary of signals that can represent the data with a sparse code. The learning problem is framed as a stochastic optimisation: minimising the expected sparse-coding cost of the dictionary. The algorithm accesses the data in batches of samples, computing the optimal sparse code on a batch. The dictionary is then fitted to minimise the cost between the observed samples and the corresponding code. Importantly, this minimisation uses the code obtained along the previous iterations of the algorithm by simply storing sufficient statistics. Hence, the algorithm is both fast and light on memory.

Figure 1: Dictionary learning to decompose brain activity in regions: visual comparison of fitting all the data with the original Mairal 2010 algorithm, and two strategy to reduce time: fitting 1/24th of the data with the same algorithm, or fitting half of the data with the new algorithm with a subsampling of 1/12. For the same gain in computation time, the approach with the new algorithm gives region definitions that are much closer to fitting the full data than reducing the amount of data seen by the original algorithm.
A subsampled version: online matrix factorisation in high dimension
Our algorithm builds upon this state of the art with an important modification: for each batch, it accesses only a random fraction of the features and updates only the corresponding entries of the dictionary. The intuition behind this subsampling is that for high-dimensional signals, there is often a certain amount of redundancy in the information. Subsampling by a given ratio of the features reduces the computation time for each iteration by the same ratio. However, it may introduce noise in parameter updates and its impact on convergence speed must be evaluated empirically. Importantly, as each iteration of the algorithm uses a different randomly chosen set of features, this noise is expected to average out.
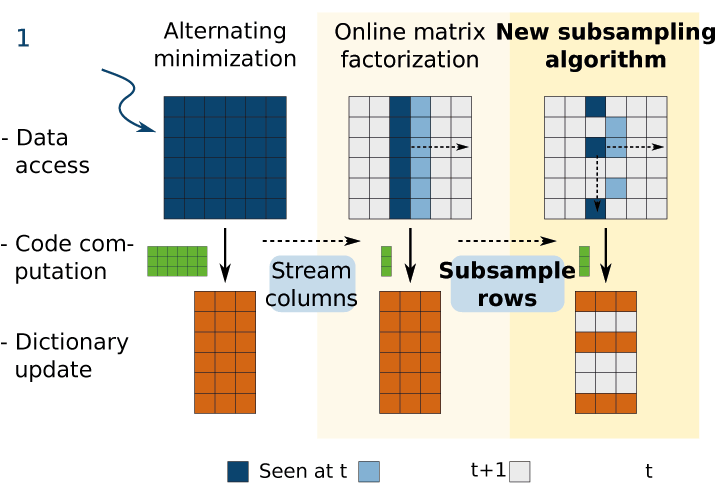
Figure 2: Schema of the algorithmic improvements: the online algorithm access the data by a stream, computing only small portions of the code at each iteration. The new algorithm also subsamples rows, updating only a fraction of the dictionary at each iteration.
Empirical results: large speedups for large data
In [1], we benchmarked this subsampling-based algorithm on two applications: 2Tb of fMRI images and movie-recommendation datasets, the largest being the Netflix data with 140 million ratings. On images, we find that the subsampled algorithm is much faster at learning a dictionary that minimises the sparse-coding cost on left-out data. For collaborative filtering on movie ratings, it converges faster to small errors on left-out data. The gain in convergence time is of the order of the subsampling ratio supported by the dataset: larger data come with more redundancy. We have recorded speed gains from a factor of 6 to 12. Additional benchmarks, soon to be published, show similar speedups on hyperspectral images, where dictionary learning is used to learn a representation of images patches for denoising or classification. Proofs of convergence of the subsampled algorithm require averaging several passes over the data (results in press).
In summary, our algorithm relies on subsampling inside an online solver for matrix factorisation. On very large data, this strategy brings up to 10-fold speedups for problems such as sparse dictionary learning or collaborative filtering. The larger the data, the more pronounced the speedups. With the trend of increasing data sizes, these progresses will likely become important in many applications.
References:
[1] A. Mensch et al.: “Dictionary Learning for Massive Matrix Factorization”, ICML (2016): 1737-1746.
[2] J. Mairal et al.: “Online learning for matrix factorization and sparse coding”, J. Machine Learning Research 11 (2010), 19-60.
Please contact:
Arthur Mensch, Inria, France











