by Nicola Viganò (CWI)
The vast majority of metallic and ceramic objects have a granular microstructure, which has a direct influence on their mechanical behaviour. Understanding the microstructure of these materials is especially important for nuclear reactors and other safety-critical applications in which they are used. Modern mathematical tools and recent developments in computed tomography can be used to study the evolution of these materials when they are being deformed or heated.
The ability to retrieve volumetric information about the crystallographic grain microstructure is necessary for understanding the initiation of damage and for establishing safety margins in critical applications. An interesting example is presented in [1], where the authors study the propagation path of corrosion cracks through polycrystalline steel samples (i.e., the materials used for the vessels of nuclear reactors), using a non-destructive three-dimensional orientation imaging technique, called diffraction contrast tomography (DCT), in conjunction with traditional X-ray absorption computed tomography.
Each crystalline object, when illuminated with X-rays, deflects some of the incoming photons whenever one of its crystal planes is oriented in a way that satisfies the famous Bragg law.
If captured on a high resolution X-ray imaging detector close to the sample, these diffracted beams form projected images of the diffracting object, which are called diffraction spots.
DCT is an X-Ray diffraction technique that uses the diffraction spots of each individual grain, in polycrystalline samples, to build a three-dimensional map of its grain microstructure.
DCT is naturally well suited for fast acquisitions, due to the use of extended beam sizes, which can capture large portions of the samples in a single scan. This makes it a good candidate for in-situ deformation studies where many deformation steps are applied to the test samples during the course of an experiment. However, traditional DCT assumes nearly perfect recrystallization of the materials, meaning that the internal deformation of the individual grains can be considered negligible. This imposes a strong limitation of applicability: real-world materials are often affected by several degrees of residual intragranular deformation, and the study of such deformation is the aim of the aforementioned type of in-situ experiments.
To adequately model and reconstruct plastically deformed grains, which exhibit rotations of the local crystal lattice, we developed a new mathematical framework in [2]. In this framework, each grain volume is defined over a six-dimensional space resulting from the merge of the classic three-dimensional Euclidean position-space, with a more exotic three-dimensional orientation-space, called Rodrigues-space, used for the representation of local crystal orientations. Unfortunately, DCT can normally provide much less data than is needed for the correct reconstruction of this six-dimensional problem, rendering it heavily under-determined. For this reason, in this framework, the reconstruction is expressed in the form of a minimisation problem, which allows for additional priors in the reconstruction. These priors can enforce some known features of the reconstructed grains, and notable examples are the famous l1-norm and total variation functionals.
While this new mathematical framework proved very effective on simple reconstructions of isolated grains, its real potential was discovered in [3]. In this study, the reconstruction was applied to extended regions of the sample, containing multiple related grains, but without having precise a-priori knowledge on the extent and morphology of the analysed region in orientation-space.
In fact, for DCT to be able to reconstruct the individual grains as a traditional oblique-angle tomography problem, it is necessary to first identify the diffraction spots belonging to each grain (indexing), which in turn allows extraction of the needed information about their centres of mass, average orientations, and bounding boxes in the six-dimensional position-orientation space.
In the case of increasingly deformed or textured materials, the indexing procedure starts to fail due the related increasing overlap on the detector between the diffraction spots belonging to different grains. This results in missing the identification of some of the grains, and as a consequence to holes in the final grain-maps. By instead allowing the reconstruction of larger regions of the position and orientation spaces, these missing grains can be reconstructed, reducing the need for an accurate indexing step. A good example is shown in Figure 1, which presents the surface orientation map of a rock-salt sample, reconstructed in Figure 1a by means of Electron Backscatter Diffraction (EBSD), a (2D) surface technique, providing the reference-result, and then by traditional 3D-DCT plus a post-processing grain-dilation step (1b), single-grain 6D-DCT (Figure 1c), and finally the multi-grain 6D-DCT (Figure 1d).
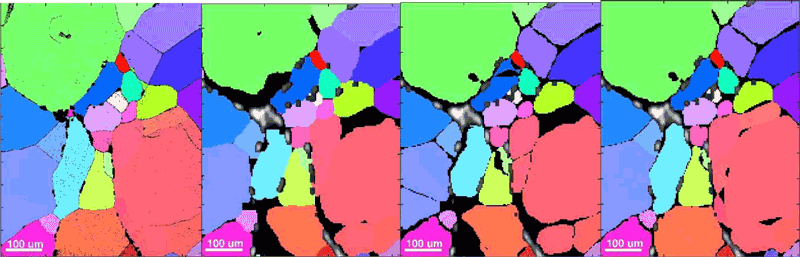
Figure 1: Orientation map of the surface of a rock-salt sample, by means of EBSD (a), 3D-DCT followed by grain dilation (b), single-grain 6D-DCT (c), and multi-grain 6D-DCT where new grains were identified by the reconstruction (d).
While the scale of applicability of this formulation is limited by the memory and computational requirements of a full six-dimensional sampling of the reconstruction-space, we expect the size of the addressable problems to continuously rise in the future, thanks to the continuous increase in computational power and memory density of modern computer technology. This, in conjunction with the fast acquisition speed provided by DCT, and the continuous evolution of the mathematical tools to address more complicated problems, will create the possibility to perform time-lapse observations of plastic deformation, coarsening, phase transformation and crack propagation in polycrystalline structural materials.
Link:
[L1] https://sourceforge.net/projects/dct/
References:
[1] A. King, et al.: “Observations of Intergranular Stress Corrosion Cracking in a Grain-Mapped Polycrystal”, Science (80..), vol. 321, no. 5887, pp. 382–385, 2008.
[2] N. Viganò, W. Ludwig, K. J. Batenburg: “Reconstruction of local orientation in grains using a discrete representation of orientation space”, J. Appl. Crystallogr., vol. 47, no. 6, pp. 1826–1840, Oct. 2014.
[3] N. Viganò et al.: “Three-dimensional full-field X-ray orientation microscopy”, Sci. Rep., vol. 6, Feb. 2016.
Please contact:
Nicola Viganò
CWI, The Netherlands
+31 (0)20 592 4176











