by Bruno Levy (Inria)
Recent research results at the junction between mathematics and computer sciences raise the possibility of new computational tools with many possible applications in data analysis, computer graphics and computational physics.
Optimal transport is a domain of mathematics that studies functions that minimise a certain cost and that satisfy a volume preservation constraint. It is very general, and can be used to model a wide class of problems. An efficient numerical solution mechanism is likely to be beneficial to a wide range of applications, comprising data and image analysis, histogram matching, computer graphics and computer animation. It has rich and interesting links with theoretical physics that make it possible to envisage the development of novel numerical simulation algorithms. These new algorithms are expected to be both more efficient and more accurate, by exploiting foundations that are at the intersection between mathematics, physics and computer sciences.
Gaspard Monge is considered the founder of optimal transport in the time of the French revolution. But the mathematical tools required to characterise existence and uniqueness had to wait until World War II, for Leonid Kantorovich (winner of the Nobel Prize in Economics in 1975) to discover the theory of duality. Recently optimal transport has generated renewed interest in the mathematics research community, under the influence of mathematicians such as Yann Brenier [1] and Cédric Villani [2].
Optimal transport is a concise and elegant mathematical language, well-adapted to express certain laws in physics, such as the least action principle and conservation laws. Moreover, the manipulated mathematical objects are very general, and encompass not only ‘smooth’ ideal objects such as continuous functions, but also less regular ones such as probability measures. The latter can be used to formalise discrete objects, such as point sets or meshes manipulated in computer science.
This generality makes it possible to directly translate the mathematical description of optimal transport into computer language without losing any properties in translation.
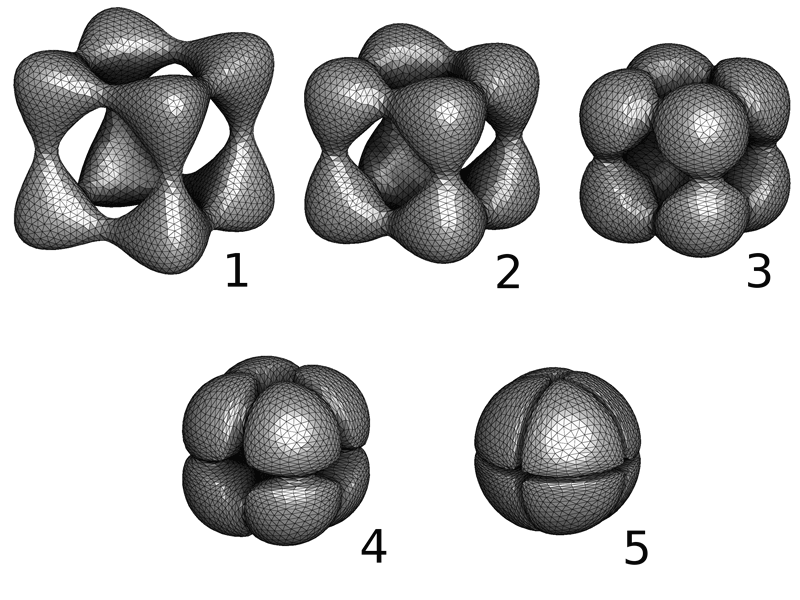
Figure 1: Optimal Transport between a shape and a sphere computed by the 3D semi-discrete algorithm.
Online demo: http://homepages.loria.fr/BLevy/GEOGRAM/vorpaview.html
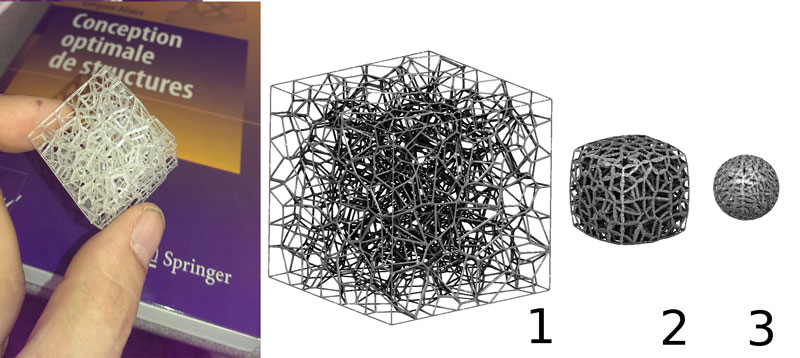
Figure 2: Selective Laser Sintering (SLS) 3D printing technology offers the possibility of creating structured materials with fine-scale geometric details. Optimal transform simulates the deformation of a ‘foldable’ cube into a sphere while preserving the volume at each step of the deformation.
The ALICE and MOKAPLAN teams at Inria are currently developing efficient numerical algorithms that can be used to solve optimal transport in a computer. They recently designed the very first ‘semi-discrete’ solver first in 2D [3] then in 3D [4] (see Figure 1). Such a solver is envisioned to become a fundamental ‘building block’ for a new class of numerical simulation algorithms, with conservation laws and the least action principle hardwired in its ‘DNA’. These two teams currently study applications in computational fluid dynamics [5] in optics, in astrophysics and in material sciences where it can be used to model the deformations of 3D-printed structured materials [6] (see Figure 2). The early numerical experiments indicate a performance acceleration factor of several orders of magnitude.
Leveraging the full power of the method and making it usable in the widest possible range of applications requires further research, both in the geometric part of the algorithm to take into account arbitrary costs besides the L2 cost and in the numerical part of the algorithm to maintain its good speed of convergence even when encountering irregularities.
References:
[1] Y. Brenier: “Polar factorization and monotone rearrangement of vector-valued functions”, Communications on Pure and Applied Mathematics, 1991.
[2] C. Villani: “Optimal Transport Old and New”, Springer, 2008.
[3] Q. Mérigot: “A multiscale approach to optimal transport”, Computer Graphics Forum, 2011.
[4] B. Lévy: “A numerical algorithm for L2 semi-discrete optimal transport in 3D”, ESAIM Mathematical Modeling and Analysis (M2AN), 2015.
[5] T. O. Gallouët, Q. Mérigot: A Lagrangian scheme for the incompressible Euler equation using optimal transport, 2016.
[6] J. Martínez, J. Dumas, S. Lefebvre: “Procedural Voronoi Foams for Additive Manufacturing, ACM Transactions on Graphics, in Proc. Of SIGGRAPH 2016.
Please contact:
Bruno Levy
Inria and LORIA, Université de Lorraine











