by Marco Attene and Giulio Ottonello
Computational geometry is not just a tool for computer graphics - its applications in Material Science are opening unexpected possibilities and exciting new research challenges.
The ability to predict the properties of new materials is of great importance in the study of natural processes such as the evolution of magma bodies and volcanic eruptions. In October 2009, the Institute for Applied Mathematics and Information Technologies (IMATI) of the Italian National Research Council began a collaboration with the Earth Science Department (Dip.Te.Ris.) of the University of Genova (Italy).The objective of this collaboration was to develop new tools for the visualization of the so-called “descent lines” that describe the crystallization of molten materials subject to heat loss. During this research, the Shape Modelling Group at IMATI also applied its expertise in computational geometry to several other applications in the field, going far beyond the original intentions.
A number of the models used to study materials are characterized by variables that turn the investigation into a multi-dimensional problem. It is common practice in Material Science to treat multi-dimensional problems using numerical techniques, performing the analysis on a finite set of samples (input data). IMATI and Dip.Te.Ris., however, have developed alternative approaches that have proved to be more robust, more efficient and, most importantly, more scalable than traditional techniques. Until now, only the behaviour of mixtures consisting of no more than three pure components could be comprehensively simulated. Using these new approaches, mixtures of any number of components can be treated, which makes it possible to simulate complex materials such as magma bodies.
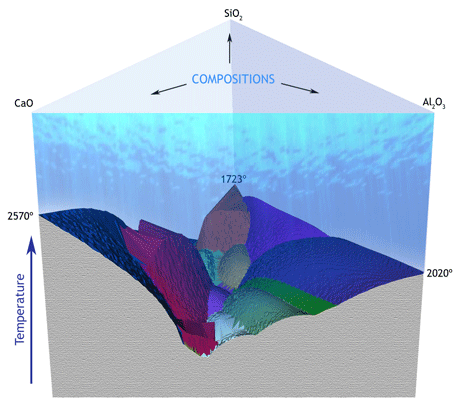
Figure 1: The liquidus of a mixture of three pure components (CaO, Al2O3, SiO2) as computed by the algorithms developed during the project.
Many interesting materials studied today are mixtures of several pure components. Typically, in Material Research the absolute amount of pure components constituting a complex material is not very important, it is much more interesting to know their relative amount. For example, “pseudowollastonite” is always composed of 50 % calcium oxide and 50 % silicon dioxide in molar proportions, independently of the bulk amount of the substance. In many cases, the characteristics of a mixture can be derived from the characteristics of its components, their relative amount, and a number of other variables such as the temperature or pressure. It is often useful to know, for example, the minimum temperature at which a given material begins to melt. On the contrary, when lowering the temperature, it is useful to know at which point a liquid substance begins to crystallize (eg at sea level, water becomes ice at zero degrees). The temperature for incipient crystallization depends on the crystallization temperature of the constituting pure components, but this dependence is not necessarily a linear combination. The mathematical function which associates each possible mixture of a given set of components to its crystallization temperature is called the “liquidus”.
The study of computer algorithms to model and analyse geometric information (i.e. computational geometry) is clearly useful to understand the liquidus which is, in mathematical terms, a “hypersurface”. In Computer Graphics, the surface of a 3D object is typically represented by a mesh of triangles, and a number of theories and algorithms exist to deal with such a geometric model. Analogously, the liquidus is a hypersurface in a space of N dimensions and, as such, can be described as a “simplicial mesh”, which is a generalized version of the triangle mesh. On the basis of this representation, IMATI and Dip.Te.Ris. are now studying methods both to compute the liquidus itself and to analyse it, independently of the dimension of the space.
In particular, each possible composition of N pure components is represented as a point within an (N-1)-dimensional simplex (ie a triangle when N=3, a tetrahedron when N=4, …). In such a simplex, convex hulls are used to derive samples of the liquidus which are then interpolated through a lifted Delaunay triangulation. The triangulation is made of simplexes of dimensions ranging from 0 to N-1, and each of them is associated with a vector specifying the direction that a line of descent must follow when passing through that simplex. On this dimension-independent model it is possible to robustly compute descent lines describing the crystallization path induced by heat loss for any initial composition.
Due to the promising results of this first year of activity, IMATI and Dip.Te.Ris. plan to keep collaborating with the objective of developing new computational tools and software libraries to support the analysis of complex materials using strongly-established geometric techniques and novel advanced shape analysis tools.
The research is expected to have a significant impact in particular in Earth Sciences, where a complex problem such as the evolution of magma bodies subjected to ascent dynamics within the Earth’s mantle becomes manageable.
Links:
Shape Modeling Group at IMATI: http://www.ge.imati.cnr.it/ima/smg/home.html
Geochemistry Lab at Dip.Te.Ris: http://www.dipteris.unige.it/geochimica/indexen.html
Please contact:
Marco Attene
IMATI-GE/CNR, Italy
Tel: +39 010 6475691
E-mail:
Giulio Ottonello
Dip.Te.Ris, Univ. Of Genova
Tel: +39 010 3538136
E-mail:










