by Vangelis Sakkalis and Ioannis G. Tollis
Recent research has exploited graph theory in the development and implementation of an advanced electroencephalogram (EEG) analysis framework for modelling and visualizing cognitive brain functions under normal or pathological conditions. There is special interest in using graph theory to study brain networks, since it offers a unique perspective to the study of local and distributed brain interactions.
Most brain disorders and cognitive brain functions remain largely unresolved. Imaging modalities like positron emission tomography (PET) and functional magnetic resonance imaging (fMRI) are valuable tools in identifying activations localized to specific brain regions (lobes). However, in comparison to classical electrophysiological techniques like the EEG, which capture the electrical activity that define neuronal communication, they represent indirect measures of neural activity and are characterized by rather poor temporal responses. All of these approaches focus on identifying the exact location of activations in the brain, which is a vital step towards understanding the brain's internal function. Modelling dynamic and synchronization phenomena in the brain will hopefully explain "how" psychological mechanisms function.
Cognitive tasks require the integration and constant interaction of widely distributed neuronal areas over the brain. The study of functional relationships and synchronization between pairs of brain regions has therefore been one of the main aims of the EEG. A variety of analysis frameworks are available that are able to capture such interdependences, ranging from linear (ie correlation and coherence) to nonlinear chaos-related ones (ie phase and generalized synchronization). Their application in the area of brain analysis is based on the assumption that the higher the synchronization, the stronger the functional relationships between the related brain regions. They are extensively used in studying the interrelationships between different cortical regions with respect to sensory stimulation, voluntary movements, the effects of drugs and a wide range of clinical and cognitive problems and tasks. In particular, higher frequency bands (ie gamma bands) are believed to reveal large-scale oscillations that enter into precise phase-locking over a limited period of time. This is often referred to as a phase-synchrony phenomenon. Another example is thought to be the genesis of epileptic phenomena, where synchrony has long been considered to be an important factor. Chaotic descriptors of the EEG were found to change through the different sleep stages and during the performance of various cognitive tasks. Nevertheless, such techniques may reveal linear and nonlinear structures that are hidden to the neurophysiologist, for whom visual signal trace inspection still remains the main diagnostic tool.
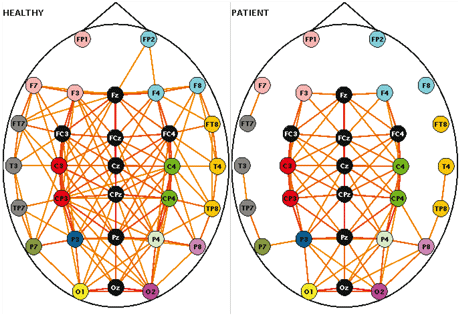
Using the interdependence methods and measures discussed in the previous paragraph, one is able to characterize and measure the coupling of complex brain networks by means of graph theory. Graph theoretical measures and visualizations provide the tools with which to study and model both local and long-range brain interactions. Measuring some basic properties of a complex network is the first step towards understanding its structure. The next step is the creation of a simulated version with similar properties, ie a mathematical model with a topology of statistical properties similar to the brain.
With this in mind, our first application was a study of the "disconnection syndrome" as proposed for schizophrenia, using graph theoretical measures and visualization. An experiment on working memory was undertaken using the gamma band (the EEG frequency of around 40 Hz), which is activated during the connecting activity (ie the "binding" of the neurons). We analysed multichannel EEG data collected from twenty stabilized patients with schizophrenia and controls, and the spatial pattern of functional connectivity was assessed by computing the wavelet coherence of EEGs. This method, as with other synchronization measures, yields a statistical coherence measure ranging from 0 to 1, which is an indication of how strongly a specific electrode is correlated with every other electrode. Thus, we obtain an NxN coherence matrix C with entries ranging from 0 to 1 formulated per task and subject. In order to obtain a graph from a coherence matrix, it must first be converted into an NxN binary adjacency matrix, A. To achieve that we define a variable called the threshold T, such that T element of [0, 1]. The value A(i,j) is either 1 or 0, indicating the presence or absence respectively of an edge between channels i and j. That is, A(i,j) = 1 if C(i,j) > T, otherwise it is equal to 0.
Using graph theoretical analysis we found that the integration related to the "binding" phenomenon, as expressed by the high-frequency gamma band, is reduced overall in schizophrenics.
In the future, higher cognitive functions like mathematical reasoning and common pathologies such as epilepsy will be investigated. Brain modelling will be further elucidated by investigating brain functional graphs during the evolution from neonate to early childhood.
The era of bioinformatics poses many challenging computational problems. Graph theory together with the advent of nonlinear synchronization algorithms point towards the synergistic research and development of quantitative techniques in the area of EEG signal analysis and visualization, which gives us an extra window of understanding into how the brain works.
This work was initiated from the Institute of Computer Science - FORTH in collaboration with the Technical University of Crete (TUC). Most of the synchronization algorithm implementations took place in the context of the BIOPATTERN Network of Excellence EU project (http://www.biopattern.org). Physical and clinical reasoning was performed in collaboration with the Clinical Neurophysiology Laboratory (Faculty of Medicine) of the University of Crete in Greece.
Link:
http://www.ics.forth.gr/bmi/
Please contact:
Vangelis Sakkalis and Ioannis G. Tollis
ICS-FORTH, Greece
Tel: +30 2810 391448
E-mail: sakkalis![]() ics.forth.gr, tollis
ics.forth.gr, tollis![]() ics.forth.gr
ics.forth.gr










