by Xavier Pennec
Understanding and modelling the individual anatomy of the brain and its variability over a population is made difficult by the absence of physical models for comparing different subjects, the complexity of shapes, and the high number of degrees of freedom implied. This also raises the need for statistics on objects like curves, surfaces and deformations that do not belong to standard Euclidean spaces. Applications are very important both in neuroscience, to minimize the influence of the anatomical variability in functional group analyses, and in medical imaging, to better drive the adaptation of generic models of the anatomy (atlas) into patient-specific data.
The shape of the brain differs greatly from one subject to another. At the scale of decimetres, a few tens of cortical folds (sulci) separating the main brain areas can be found consistently in all subjects, although they are geometrically very variable. At lower scales, however, many more sulci can be only partially matched across subjects and it is difficult to speak about their homology. Computational anatomy, an emerging discipline at the interface of geometry, statistics and image analysis, aims to analyse and model this type of biological variability at the population scale. The goal is not only to model the normal mean anatomy and its normal variations among a population, but also to discover morphological differences between normal and pathological populations, and possibly to detect, model and classify pathologies from structural abnormalities. Another goal is to correlate this variability information with other functional, genetic or structural information (eg fibre bundles extracted from diffusion tensor images). Important applications include the spatial normalization of subjects in neuroscience (ie mapping all the anatomies into a common reference system) and atlas-to-patient registration in order to map generic knowledge to patient-specific data. Computational anatomy is currently a very active research field, as exemplified by the very successful workshop on the Mathematical Foundations of Computational Anatomy (MFCA'06), organized in September 2006 in conjunction with the conference MICCAI'06.
Many geometrical and physically based registration methods exist that can faithfully deal with intra-patient deformations. However, the absence of physical models relating the anatomy of different subjects leads to a reliance on statistics to learn the geometrical relationship from many observations. The method is to identify anatomically representative geometric features (points, tensors, curves, surfaces, volume transformations), and to model their statistical distribution. This can be done, for instance, via a mean shape and covariance structure after a group-wise matching. However, the features usually belong to curved manifolds rather than to Euclidean spaces, which precludes the use of classical linear statistics. For instance, the average of points on a sphere is located inside the sphere and not on its surface. We were among the first to propose a consistent set of statistical tools to work on Riemannian manifolds (mean value, covariance matrix, Normal law, Mahalanobis distance) along with efficient algorithms and tractable approximations for small variances. We used this framework with P. Fillard to infer anatomical variability in the context of the INRIA-associated team BrainAtlas with P. Thompson at LONI. We proposed to model the variability of the brain from a dataset of precisely delineated anatomical structures (sulcal lines) on the cerebral cortex. We model the first- and second-order moments of sulci by an average sulcal curve and a sparse field of covariance tensors along these curves. The covariance matrices are then extrapolated to the whole brain using a harmonic diffusion PDE on the manifold of tensor fields. As a result, we obtain a dense 3D variability map, which proves to be in accordance with previously published results on smaller samples of subjects. Statistical tests demonstrated that our model was globally able to recover the missing information. Preliminary results on the correlation between local and distant displacements indicate that the displacement of the symmetric point is correlated. Other long-distance correlations also appear, but their statistical significance still needs to be established.
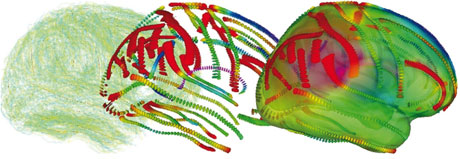
Another way to gather statistics on inter-subject brain variability is to perform multiple deformable registrations between a reference image and subject images. We recently proposed a consistent mathematical framework called Riemannian elasticity to learn the shape deformation metric from a set of registrations and to use the result as a regularization penalization for new non-rigid registrations. First experiments indicate that the method is sound and effective. Other methods are currently being investigated by other groups. However, due to the very high complexity of the problem, each team is targeting specific aspects with different types of anatomical features and different statistical methods. In order to compare and combine wherever possible the algorithmic solutions and the databases for the statistical estimation, we recently initiated the INRIA Cooperative Research Initiative BrainVar with the Neurospin initiative (http://www.neurospin.org) and several other groups in France including LENA (laboratory for cognitive neurosciences and cerebral imaging at Hopital la Pitié-Salpêtrière, Paris), the Visages (vision, action and information management system in health) INRIA-INSERM reserach team at Rennes (http://www.irisa.fr/visages/visages-eng.html), LSIS (laboratory of information science and systems), Marseilles, and CMLA (centre for mathematics and its applications, Ecole Normale Superieure de Cachan). We plan to investigate many sources of information: cortical landmarks like sulcal ribbons and gyri, the surface of internal structures or fibre pathways mapped from DTI. Individually, these sources of information provide only a partial and biased view of the whole variability. Thus, we expect to observe a good agreement in some areas, and complementary measures in other areas. This will most probably lead in the near future to new neuroanatomical findings and more robust medical image analysis applications.
Links:
http://www-sop.inria.fr/asclepios/
The ARC BrainVar: http://www-sop.inria.fr/asclepios/projects/ARCBrainVar/
Please contact:
Xavier Pennec
INRIA, France
Tel: +33 4 92 38 76 64
E-mail: xavier.pennec![]() sophia.inria.fr
sophia.inria.fr










