by Olivier Clatz, Ender Konukoglu, Pierre-Yves Bondiau, Simon Warfield, Hervé Delingette and Nicholas Ayache
Computational models of brain tumor have gained attention among scientists in the last decade. Equations describing these models now include different components of the growth: cell proliferation, migration through the tissue and expansion. Recent efforts were devoted to the inclusion of patient-specific data into the model. Simulation results demonstrate a good correlation with radiological observations and allow for new perspectives in neuro-oncology.
Brain tumors show a complex pattern of growth at a cellular level. At histological scale, two major mechanisms are responsible for the invasion of the tumor: infiltration and expansion. Infiltrating tumor cells are isolated cells that invade the brain through a diffusion process. This diffusion tends to follow white matter fibers. Expansion describes the coherent growth of the tumor mass, pushing surrounding structures away. Most of the diffusive brain tumors (known as gliomas) share these 2 patterns of growth, with different proportions depending on their grade.
Biomathematical Models
Different mathematical models have been developed at different scales to model the growth of gliomas. For example, cellular automata describe the evolution of tumors at the microscopic scale. The models we develop in the Asclepios project of INRIA Sophia Antipolis describe the tumor at the macroscopic scale, corresponding to the observation scale in medical images. In our model, the evolution of tumor cell density is described with a reaction-diffusion equation. This equation involves two parameters: r and D, which respectively control the speed of cell division and diffusion into the tissue. In our case, the diffusion tensor D takes into account the anisotropic invasion of tumor cells in the white matter fibers. This equation is coupled to a mechanical equation to model the mass effect of the tumor. It is important to notice that the numbers of parameters have intentionally been kept small in this model, to minimize the number of unknowns to fit to the data.
These two equations completely describe the three components of the tumor growth: proliferation, diffusion and expansion. Different properties are set according to the different tissues of the brain, identified on MR images of the patient. Specific boundary conditions prevent tumor cells from diffusing through the skull and ventricles. This personalized model allow for a realistic simulation of the tumor growth with respect to observations (see Figure 1).
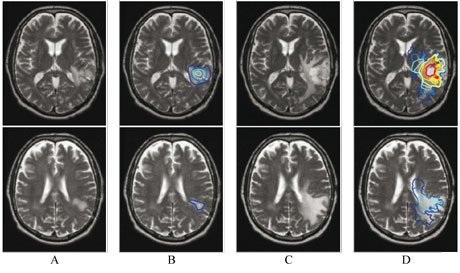
Applications
In the context of the associated team CompuTumor and the European project Health-e-Child, we are currently developing methods to identify model parameters based on radiological images of the patient. These methods allow for a personalized and quantitative diagnostic of the pathology. Such information could influence the therapeutic strategy: a very diffusive tumor (high D, low r) may be better treated with extended radiotherapy and chemotherapy, while surgery seems more adapted to expansive -but less diffusive- tumors.
This model could also provide information that cannot be quantified by MRI. Indeed, it allows for the estimation of the local tumor cell density, where the MR image only shows a detection threshold. By better defining the invisible part of the tumor, this may open new possibilities for the treatment of these tumors with radiotherapy. Figure 2 presents a synthetic example of the application of the model to radiotherapy. The simulated virtual tumor of this example illustrates the improvement in the radiotherapy margin definition in the case where the extension of tumor cells matches that simulated with a growth model.
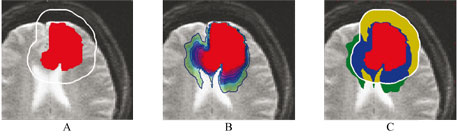
Links:
Asclepios research project: http://www-sop.inria.fr/asclepios/
CompuTumor associated team: http://www-sop.inria.fr/asclepios/projects/boston/
Health-e-child: http://www.health-e-child.org/
Please contact:
Olivier Clatz
INRIA, France
E-mail: olivier.clatz![]() sophia.inria.fr
sophia.inria.fr










