Afivo – A Framework for Efficient Parallel Computations with Adaptive Mesh Refinement

by Jannis Teunissen (CWI and KU Leuven) and Ute Ebert (CWI and TU/e)

We have developed a framework for efficient 2D and 3D computations on adaptively refined grids, which can be used on shared-memory computers. By using efficient methods, we aim to make interactive (quick!) simulations possible on modest hardware.

Some physical systems evolve on widely different spatial and temporal scales. Computer simulations of such systems can often be sped up by many orders of magnitude if the resolution of the simulations is cleverly varied in space and in time, which is referred to as adaptive mesh refinement (AMR). The use of AMR is particularly important for 3D simulations. If, for example, the resolution in a region is reduced by a factor of four, the number of unknowns is reduced by a factor of 64 (four cubed)!

For computationally expensive simulations, a balance has to be struck between adaptivity and performance. CPUs and GPUs work most efficiently when they are given structured data, for which nearby values in space are also nearby in the computer's memory. This is the reason that “structured” adaptive mesh refinement is popular. With structured AMR, an adaptive mesh is constructed from smaller grid blocks that are individually suitable for efficient computing. A list of frameworks for structured AMR is given in [L1]. Of course, such frameworks also employ parallelization, and many of them are aimed at large-scale simulations on super-computers.

Since 2015, the Multiscale Dynamics group at CWI has been busy developing yet another framework for structured AMR simulations, called Afivo [1][L2]. One of the distinctive features of Afivo is that it employs shared-memory parallelism (using OpenMP), and no distributed-memory parallelism (using MPI), which is common in other frameworks. This makes it simpler to implement and test new AMR algorithms, because there is no need for load balancing or explicit communication between processes. On desktops or single compute nodes, shared-memory parallelism also tends to improve performance. The drawback is of course that the framework cannot be used on distributed-memory systems.

Other key features include the bundled geometric multigrid methods, which can be used to rapidly solve elliptic partial differential equations such as Poisson's equation. These methods are ideally suited to structured AMR computations, and on current hardware we can achieve solution times below 10 nanoseconds per unknown. This means that simulations with up to hundreds of millions of unknowns can be performed on desktops or single compute nodes. For the visualisation of the corresponding AMR data, output in an efficient data format is supported.

Application: Simulating Electric Discharges
In our group, we study electric discharges, which are prominent examples of multiscale phenomena. An example is shown in Figure 1. A lightning strike can be kilometres long, but its growth is made possible by much smaller plasma channels that are perhaps only a few decimetres long and millimetres wide. These smaller channels are called streamer discharges, and they in turn contain structures that are only a few micrometres in size. Being able to simulate streamer discharges is not just important to understand lightning, but also because they occur (and are used) in many high-voltage applications.

Figure 1: If we could keep zooming in on lightning strikes, we would eventually see streamer discharges (the centimetre-long channels on the right). [Image credits from left to right: John R. Southern, P. Kochkin, T. Briels].

Based on the Afivo framework, we have developed a code to efficiently simulate streamer discharges. An example of a 3D simulation is shown in Figure 2. The ratio between the domain size and the finest mesh spacing is typically about four orders of magnitude; the ratio between simulation time and the time step is similar. A big advantage of having an efficient AMR simulation code is that smaller (2D) simulations can be performed in minutes instead of hours or days [3]. This allows for a much more interactive investigation of the simulated system, which we think is crucial in making computer simulations a viable alternative and complement to lab experiments.

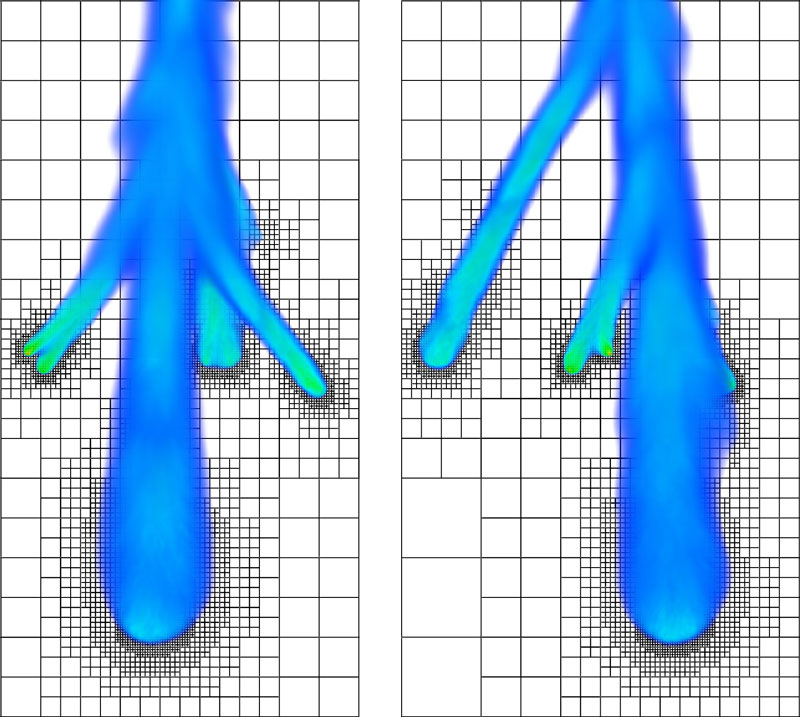
Figure 2: Two views at an angle of 90° on the electron density in a 3D streamer discharge simulation [2] [L3], with the numerical grid projected underneath. Each visible grid cell actually corresponds to a mesh block of 8x8x8 cells. The computational grid contains tens of millions of cells, and changes frequently to track the developing discharge channels.

Outlook
Thus far, we have focused our efforts on efficient computations in simple geometries (e.g., rectangular computational domains). In the coming years, we aim to add support for the embedding of curved objects like electrodes, insulators or droplets, while keeping the computational efficiency high.

References:
[1]  J. Teunissen and U. Ebert: “Afivo: a simulation framework with multigrid routines for quadtree and octree grids”, Comput. Phys. Commun. 233, 156 (2018), https://kwz.me/htR
[2]  J. Teunissen and U. Ebert: “Simulating streamer discharges in 3D with the parallel adaptive Afivo framework”, J. Phys. D: Appl. Phys. 50, 474001 (2017), https://kwz.me/htU
[3]  B. Bagheri et al.: “Comparison of six simulation codes for positive streamers in air”, Plasma Sources Sci. Technol. 27, 095002 (2018), https://kwz.me/htV

Links:
[L1] https://kwz.me/htW
[L2] https://kwz.me/htX
[L3] https://kwz.me/htZ

Please contact:
Jannis Teunissen, CWI, The Netherlands and KU Leuven, Belgium
This email address is being protected from spambots. You need JavaScript enabled to view it.