by Vagelis Harmandaris (UOC & IACM-FORTH), Evangelia Kalligiannaki (IACM-FORTH) and Markos A. Katsoulakis (UMass Amherst, USA)
The development of novel materials with desirable properties, such as nanocomposites, polymers, colloids and biomolecular systems, relies heavily on the knowledge of their structure-property relationships. The prediction of such relationships is the subject of computational materials design. Molecular dynamics (MD) simulations at the atomistic level can provide quantitative information about structural and dynamical properties of molecular systems. The recent enormous advances in computational power allow us to perform intense atomistic-level simulations. However, the broad range of length and time scales appearing in such complex (e.g., macromolecular) materials still presents significant computational challenges, especially in tackling engineering and design tasks.
Model order, or dimensionality, reduction is a standard methodology used to broaden the family of materials studied via simulations. In such a scenario, a molecular system is described by the most relevant degrees of freedom via coarse-grained (CG) models, which are developed by averaging out details at the molecular level. Typical examples involve representing groups of atoms by a single CG particle, see Figure 1.
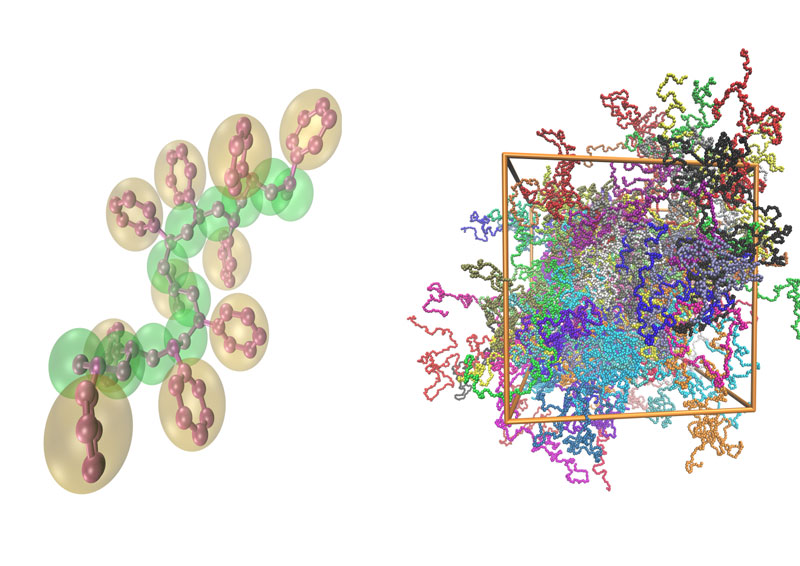
Figure 1: Caption: Model reduction (coarse graining) in macromolecules: A single polymer chain in atomistic and CG representation (left), and a snapshot of a CG bulk polymeric system (right).
We follow a systematic methodology to acquire rigorous CG models from the analysis of microscopic data, obtained from atomistic simulations. The analysis procedure involves (i) the suggestion of a parametric, or non-parametric, CG physical model, as well as (ii) the multi-dimensional fitting over datasets taken from atomistic MD simulations, i.e., it is a model- and data-based approach. The source of our simulation data is a physical model (the atomistic model), whereas the desired CG model we look for is hybrid: it involves physics-based aspects, such as the proposed type of interaction between CG variables (force field), as well as data-driven characteristics, such as the estimation of the parameters that will be inferred; this makes the CG model a “digital twin”, see Figure 2.
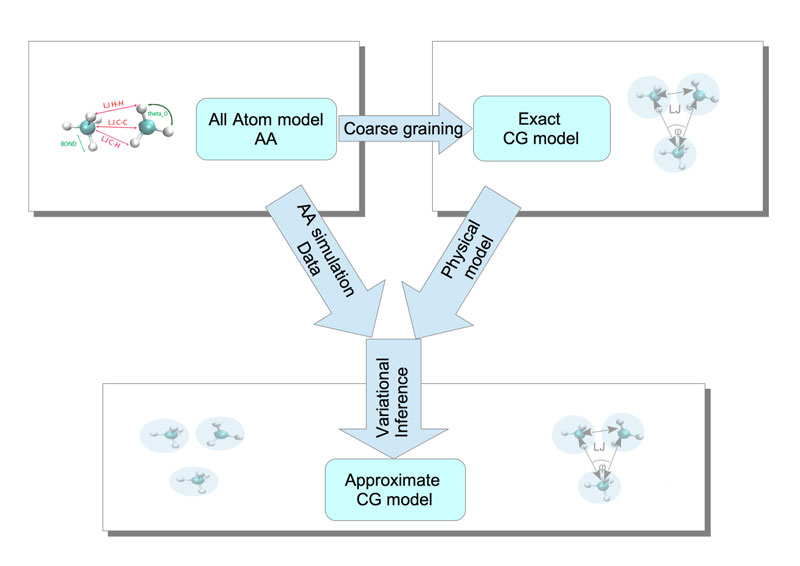
Figure 2: Caption: A schematic description of the model reduction in molecular systems and the effective CG models through variational inference.
We focus on the study of materials both at equilibrium [1] and under non-equilibrium conditions [2]. For systems at equilibrium, and near equilibrium, there is a direct connection between structural properties and CG interaction potentials (the force field in the CG level), via the potential of mean force (PMF) concept, which can be used to approximate the exact corresponding CG model. The development of rigorous CG models for materials far from equilibrium is a much more complex problem. At the same time, such systems are of great interest for most engineering applications related to nanotechnology, polymer processing, biotechnology, etc.
The challenge in the inference problems for systems out of equilibrium is that the time series data sets representing the coarse variable trajectories are both strongly correlated and relatively few, due to their high computational cost, setting up another “twin challenge”. In contrast, current machine learning methods typically address big and independent datasets. Indeed, many problems in machine learning involve classification, analysis, and predictions, using data sets of points which are independent of each other; for instance, to correctly predict the digit between 0-9, given images of handwritten characters. However, this is not the case in many applications involving physicochemical systems, where dependencies and correlations in space/time and between model elements (molecules, parameters, and mechanisms), as well as couplings between scales and physics (from quantum, to atomistic to meso/macro-scale) are the norm, rather than the exception. Moreover, although the exact CG dynamics is known and described by a stochastic integro-differential system with strong memory terms, it is computationally intractable, and approximations of the CG dynamics are essential.
Recently we have developed an optimisation approach to retrieve a best-fit approximate CG evolution model, i.e., the path-space variational inference for CG [1]. Variational inference is a central tool in machine learning where the inference problem is tackled approximately using an optimisation principle. For CG dynamics and nonequilibrium models, our optimisation principle involves the minimisation of information loss between time series, introduced by coarse-graining, between the probability distribution of the trajectories (time series data) of the coarse variables defined by the atomistic and the coarse dynamics.
This research was applied successfully to benchmarking problems, such as simple liquids, alkanes at transient and equilibrium regimes [1,2], as well as to complex reaction networks [3]. Current and future work concerns computational applications of the path-space variational inference approach to complex macromolecular systems and multi-component nanostructured materials at equilibrium as well as beyond equilibrium.
Our research team is an interdisciplinary team composed of chemical engineers and applied mathematicians. We have long-standing experience in model reduction methods, mathematical and computational modeling of complex systems, and variational inference methods, [L1, L2].
Three different institutes are involved in the research project: University of Crete (Greece), Institute of Applied and Computational Mathematics – FORTH (Greece), and UMass Amherst (USA). We also have several years’ active collaboration with research institutes worldwide.
Links:
[L1] http://macomms.tem.uoc.gr/
[L2] https://kwz.me/htQ
References:
[1] V. Harmandaris, et al.: “Path-space variational inference for non-equilibrium coarse-grained systems”, J.Comp. Phys., 314(1), 355-383, 2016.
[2] C. Baig, V. Harmandaris: “Quantitative Analysis on the Validity of a Coarse-Grained Model for Non-equilibrium Polymeric Liquids under Flow”, Macromolecules, 43, 3156–3160, 2010.
[3] E. Kalligiannaki, M. Katsoulakis, P. Plecháč: “Spatial multi-level interacting particle simulations and information theory-based error quantification”, SIAM J. Sci. Comput. 36-2, A634-A667, 2014.
Please contact:
Evangelia Kalligiannaki
IACM FORTH, Greece
+302810391891











