by Oleg Chertov and Dan Tavrov
Protection of individual online privacy is currently a high profile issue. But, as important as it is, solving individual privacy issues does not eliminate other security breaches likely to occur if data aren’t handled properly. Collective information about groups of people is also of vital importance and needs to be secured. Novel research into providing anonymity for particular groups highlights the necessity of privacy for groups.
The public is concerned about online privacy. Google’s cloud computing services collect consumer data; search engine Yahoo keeps the data about Web searches; DVD-by-mail service Netflix keeps its users’ movie records. Public awareness of these and similar cases force involved companies to improve their privacy policies.
Such a reaction is usually expected when it is necessary to preserve anonymity of a particular individual. But mining huge data collected online can violate privacy of a group of people as well. For instance, the data gathered on Facebook, if accessed and properly analysed (and this does occur), can violate privacy of a certain group of participants, even if this group is not explicit. An outstanding number of messages on a particular topic could point to a group of network members belonging to the same community, for example. This information can be valuable for tracking down criminal activities, for marketing, and so forth.
In other words, we face the problem of providing group anonymity of statistical data. Within our project conducted at the Applied Mathematics Department of the National Technical University of Ukraine “Kyiv Polytechnic Institute”, we have derived algorithms that provide group anonymity and have applied them to real statistical data. The basic features of our propositions are outlined below.
In general, providing group anonymity implies performing three steps. The dataset to be protected needs to be mapped onto appropriate data representation which can help define sensitive group data features. Then, such representation has to be appropriately modified in order to protect them. Afterwards, it is necessary to obtain modified dataset from the modified data representation.
Group anonymity heavily depends on data representation. The same dataset can be represented in many ways convenient for protecting the data against privacy breaches. Within our project, we proposed various ways of representing statistical data, each suitable for analysing particular data properties.
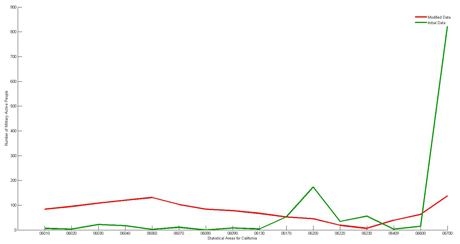
Figure 1: Numbers of active duty military personnel distributed by statistical areas of California. The green line shows the distribution computed using US population census 2000 microfile data provided by the US Census Bureau, http://www.census.gov/census2000/PUMS5.html. The red line shows distorted numbers obtained by solving the group anonymity problem using Daubechies wavelet of order 2.
To explain this, let us consider a simple procedure of counting respondents possessing certain property and living in a certain area. For illustration, we can count the number of active duty military personnel living in different areas. A graph of the data reveals areas with denser populations of military personnel. The green line in Figure 1 represents such a graph, calculated for the military personnel distributed over statistical areas of the state of California, the US (according to the US Census 2000). Extreme values in the graph inevitably indicate the location of military bases. If this information is required to be confidential, it is necessary to conceal the distribution.
One of the easiest ways to modify this data representation is to redistribute active duty military respondents by different areas to obtain a completely disseminate graph. Our research has demonstrated that an arbitrary distortion of the initial dataset leads to certain information loss which must be prevented.
We applied several methods each aiming to preserve a particular feature of the data. Wavelet analysis is a frequently used technique for splitting data into low- and high-frequency components. The low-frequency component, called “approximation”, stands for the smoothed version of the data, while the high-frequency components, referred to as “details”, tell much about intrinsic data properties. We propose to make full use of both approximation and details by playing around with the appearance of approximation which allows us to achieve the desired transformed distribution (Figure 1, red line). At the same time we leave details intact, thus guaranteeing preservation of the useful properties of the dataset.
After having obtained transformed distribution, it is necessary to accordingly modify the underlying dataset, introducing as less distortion as possible.
We intend to continue our research in the field of group anonymity to make better use of the information underlying the statistical data. In particular, we are considering applying fuzzy logic techniques to achieve anonymity, since statistical data consist mainly of various linguistic values which require proper processing.
We invite every interested ERCIM member to cooperate in conducting research in the group anonymity field which may be viewed as a logical succession of the previously completed Privacy Os-European Privacy Open Space project.
References:
- O. Chertov and D. Tavrov, “Group Anonymity,” Communications in Computer and Information Science, vol. 81, Part II, pp. 592–601, 2010.
- О. Chertov and D. Tavrov, “Data group anonymity: general approach,” International Journal of Computer Science and Information Security, vol. 8, № 7, pp. 1–8, 2010.
- O. Chertov, D. Tavrov, D. Pavlov, M. Alexandrova, and V. Malchikov, Group Methods of Data Processing, O. Chertov, Ed. Raleigh: Lulu.com, 2010, 155 p.
Please contact:
Oleg Chertov, Dan Tavrov
National Technical University of Ukraine "Kyiv Polytechnic Institute"
E-mail:










