by Juan C. Vallejo and Miguel A. F. Sanjuán
All numerical calculations have inherent inaccuracies, and beyond certain timescales even the best method will diverge from the true orbit. The concept of shadowing time allows the reliability of a computer-generated orbit to be characterized. This indicator is being applied to some models of galactic potentials, where areas of high and low predictability mix in a fractal-like way.
In the last century, the numerical approach to solving physical problems has gained in relevance with the increase of computational facilities. Methods derived from chaos theory and nonlinear dynamics techniques are quite useful in solving real problems where chaos is present and a strong dependence on initial conditions is a key issue.
Predictability refers to the assessment of the likely errors in a forecast, either qualitatively or quantitatively. It refers directly to the stability/instability of the true orbit, but also to the coincidence of the calculated orbit itself, or reliability.
Instability is a very well-known factor when considering a given solution to the model. In a broad sense, an orbit is unstable if it is strongly dependent on initial conditions. More precisely, an orbit is chaotic if the dynamics is bounded, has at least one positive Lyapunov exponent and the omega set is not periodic and does not consist solely of equilibrium points and connecting arcs. The larger the instability, the larger is the likehood that the real orbit will diverge from the calculated one.
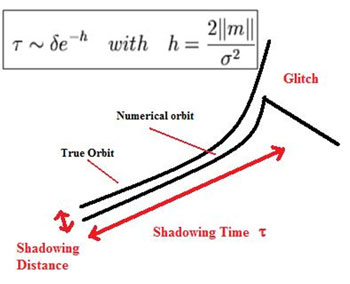
Figure 1: Computers move from one true orbit to another nearby orbit because rounding errors and internal floating number representations. How long the true orbit is shadowed by the computed orbit before suffering a glitch and later deviation can be estimated from Lyapunov exponent distribution.
Typically, the reliability time goes with the inverse of the Lyapunov exponent, or Lyapunov time. As all numerical calculations have inherent inaccuracies, beyond certain timescales even the best method will diverge from the true orbit. The usual steps for analysing a given system involve calculating the instability for a given set of initial conditions. It happens that the standard definition of the Lyapunov exponent has a very long convergence time (if any). Due to the slow convergence of the asymptotic value, many others numerical indexes are used, but the basic idea remains the same.
However, we can also refer to the numerical reliability of the system understood as the confidence of the computed orbit and the true orbit during an interval of time, independently of its instability. Essentially, computers move from one true orbit to another nearby orbit because of rounding errors and internal floating number representations. However, the computed orbit (called pseudo-orbit) may still lead to correct predictions because of the existence of a nearby exact solution. Otherwise, the calculated orbit may be very distant.
The true orbit is called a shadow, and the existence of shadow orbits is a very strong property, with the shadowing time being a valid limit for the predictability of the system. A basic requirement for shadowing is that the system be hyperbolic. In case of nonhyperbolicity, the point may not be shadowed and the computed orbit behaviour may be completely different from the true one.
Stability is not the same as hyperbolicity. An orbit can be unstable and yet hyperbolic. When the orbit is nonhyperbolic, there can be still a moderate obstacle to shadowing when the nonhyperbolicity is due to tangencies between stable and unstable manifolds. But in the so-called pseudo-deterministic systems, when nonhyperbolicity is sourced to a phenomenon named unstable dimension variability, the shadowing is only valid during trajectories of given lengths, which may be very short.
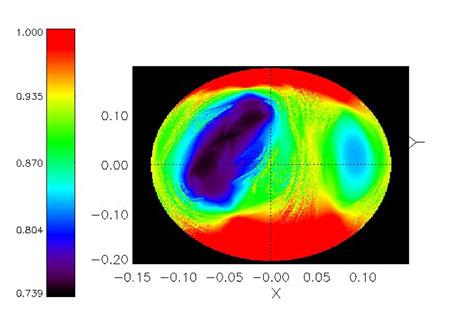
Figure 2: Plotting the instability and hyperbolicity indexes provides insight into the predictability for every initial condition of the available phase space. However, such indexes distribute in a very complex way under certain conditions of the model parameters, often showing fractal structures like those in the figure.
Our work in the Nonlinear Dynamics, Chaos and Complex Systems Group at the Universidad Rey Juan Carlos (URJC) in Madrid, is focused on analysing and plotting predictability charts for certain models. We get the shadowing times by computing the finite time Lyapunov exponent distributions. Each computational run is based on the integration of one initial condition with a well-known Runge-Kutta-Fehlberg integrator scheme. As the integration progresses, the distribution is calculated and the instability and hyperbolicity indexes are derived. This is repeated for several conditions and parameters, thus returning a complete description about the predictability of the used model.
Note that this strategy is very well suited for high-throughput (Grid) numerical schemas. A set of shell scripts feeds the integrator with the proper initial conditions and a grid engine (in our case, GridWay) and submits the process to the proper cluster in a user transparent way.
These techniques are general enough to be applied to different models with minor modifications. Our work focuses on galactic modelling, where the applied timescales are critical. Mathematically meaningful timescales cannot be physically acceptable here. A particle being shadowed during only a few crossing times (cycles) is a critical issue. Galaxies are evolutionary entities, from the point of view of both their gravitational potential and their constituents. For instance, in a Milky Way type model, the older stars will have orbited the galactic centre just sixty times before death. And the galaxy itself may evolve during this short period of time. Interpreting the dynamical system in a broad sense, given an initial condition, the stability refers to the location itself, not to the tracer particles. But considering what happens to the model in such short timescales, and for the sake of our discussion, the forecast of the numerical galactic model reliability is then of importance.
Link: http://www.fisica.escet.es
Please contact:
Juan C. Vallejo
Universidad Rey Juan Carlos, Madrid, Spain
Tel: +34 91 8131366
E-mail:










