by Lukáš Vácha, Jozef Baruník and Miloslav Vošvrda
‘Smart traders’ is a new concept for improving the usual models for future price movements in financial markets. The influence of the proposed smart traders concept is examined with simulations.
An important feature of heterogeneous agent models (HAM) is their ability to explain stylized facts observed in financial time series, mainly fat tails and volatility clustering. Typically, in the heterogeneous agent’s model, two types of agents are distinguished: fundamentalists and chartists. Fundamentalists base their expectations about future asset prices and their trading strategies on market fundamentals and economic factors, such as dividends, earnings, macroeconomic growth, and unemployment rates. Chartists or technical analysts try to extrapolate observed price patterns, such as trends, and exploit these patterns in their investment decisions.
We introduce a new concept – smart traders. The idea of smart traders is based on the endeavour of market agents to estimate future price movements. By adding smart traders we try to improve the original heterogeneous agent’s model so it can better approximate real markets. Smart traders are designed to forecast the future trend parameter of price deviations using information sets consisting of past deviations. For simplicity, they are modelled to assume that the price deviations, defined by the model, are an AR(1) process and they use the maximum likelihood estimation method for forecasting. Thus, in our model we use two groups of traders: smart traders and a group of stochastically generated trading strategies.
Furthermore, we introduce changes in sentiment, which we define as a shift in beliefs about the future trend of a new investor strategy on the market. This allows us to model trend-followers and contrarians. In this work we use only the form of jumps in sentiment. Our main expectation is that the introduction of smart traders and changes in sentiment will change the simulated market prices significantly.
Model
The model presents a form of evolutionary dynamics called the Adaptive Belief System in a simple present discounted-value pricing model. Simulated capital market is a system of interacting agents who immediately process new information. Agents adapt their predictions by choosing from a limited number of beliefs. Each belief (trading strategy) is evaluated by a performance measure. Agents on the capital market use this performance measure to make a rational choice that depends on the heterogeneity in agent information.
Simulation Results
The main purpose of the simulations is to examine the influence of the proposed smart traders concept and changes in sentiment on the simulated market prices. We compare the model without smart traders (0ST) with the model with five smart traders (5ST) and the model with five smart traders in the first group and changes in sentiment in the second group (5STS).
Altogether we consider 40 trading strategies for each simulation. Figure 1 shows the empirical probability density function of the trend parameter observed on the simulated market with sentiment change. It is the cross-section through the iterations, and the changes in sentiment can be clearly observed. Each model has been simulated 36 times to achieve robust results. Figure 2 shows the kernel estimation of the probability density functions (PDFs) of simulated returns.
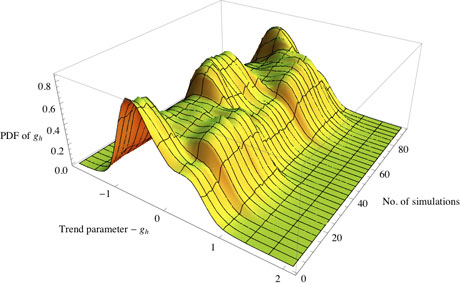
Figure 1: Empirical PDF of the trend parameter - gh on the market through the iterations with the sentiment change.
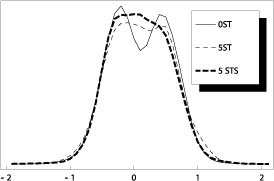
Figure 2: Empirical PDF of X(t) for simulated models without smart traders, with five smart traders, and with five smart traders and changing sentiment.
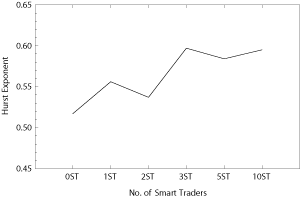
Figure 3: Hurst exponent of returns for different numbers of smart traders.
Conclusion
By adding smart traders we try to improve the original heterogeneous agent’s model so that it provides a closer description of real markets. The main result of the simulations is that the probability distribution functions of the price deviations change significantly with an increasing number of smart traders in the model, and they also change significantly when changes in sentiment are introduced. We also use the Hurst exponent to measure the persistence of the price deviations and we find that the Hurst exponent increases significantly with the number of smart traders in the simulations (see Figure 3). This means that the introduction of the smart trader’s concept into the model results in significantly higher persistence of the simulated price deviations. On the other hand, the introduction of changing sentiment in the proposed form does not change the persistence of the simulated prices significantly.
Please contact:
Lukáš Vácha - CRCIM (UTIA)
Tel: +420-266052432
E-mail:










