by Pierluigi Contucci, Cristian Giardinà, Claudio Giberti and Cecilia Vernia
Real-world phenomena are often described by complex systems with competitive and cooperative behaviour. Such systems, as much as the described phenomena, are hard to understand in a scientific perspective mainly due to the lack of general exact solutions. For cases like this, the computational sciences provide a very useful virtual laboratory. The case of disordered systems is an example of scientific computing techniques being used to test theoretical predictions and uncover new phenomena that remain unreachable by traditional analytical methods.
Complex systems made by a large number of interacting components have been studied using simplified mathematical models. A typical and paradigmatic case is the spin glass (a magnet with imitative and anti-imitative random interactions) with a rich and nontrivial structure of multiple equilibrium states. Although even the basic models are far from being solved there have been many important results, such as Parisi’s analytical solution of the mean-field Sherrington-Kirkpatrick model (SK), in which every agent interacts with all the others with the same average strength. The solution has shown that the model behaviour can be conveniently described in a compact way by a function which encodes the complex hierarchical organization of the system. Such a breakthrough has influenced the hard sciences in the last thirty years no less than Onsager’s solution (for the two-dimensional Ising model) did in the past. Combinatorial optimization (with the device of survey propagation algorithm) is among those fields that have been changed by its far-reaching consequences.
The broad generality of the spin-glass problem can be understood in a simple sociological context: consider a group of people where friends and enemies are present. When making a choice, friends tend to imitate each other while enemies tend to take opposite decisions. Individuals will experience conflicting requests and frustration due to the impossibility to satisfy all the relational constraints. There will typically be many sets of choices that minimize the total discomfort. That picture gives an idea of why simulations of spin glasses are difficult to perform. First, the problem is interesting for large numbers of individuals and second, the exploration of the entire set of optimal solutions belongs to the NP-complete class, making it a computationally hard problem (see Link 1 below).
A research group consisting of people from the Universities of Bologna, Modena and Reggio Emilia, Eindhoven and Roma has been involved in spin-glass computational study since 2003. The research project started with the development of a class of new optimization dynamical algorithms (see Link 2) which, using a suitable annealing procedure coupled with a balanced greedy-reluctant strategy drive the system towards the deepest minimum of the cost function. More recently the group started a computational study of the Edwards-Anderson (EA) model with short-range interaction and no known exact solution. The EA model is among the most interesting and unsettled problems in spin-glass theory, and the relevance of the mean-field solution to the EA model is vividly debated. Numerical investigations can be extremely useful to discriminate between the different physical pictures that have been proposed. The aim of the research has been to check whether and to what extent the EA model displays the features of the SK model, such as factorization properties, overlap equivalence, ultrametricity and decay of correlations (see Link 3). Ultrametric spaces have a striking property: the triangles (see Figure 1) constructed by joining three points have at least two equal sides and scalene triangles do not exist.
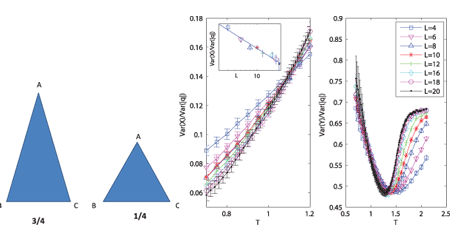
Figure 1: Ultrametricity in spin glasses. The prediction of Parisi's solution (1/4 equilateral triangles, 3/4 isosceles triangles, no scalene triangle) is checked in a short-range spin glass (picture taken from: http://arxiv.org/abs/cond-mat/0607376).
Scientific computing allows the behaviour of moderately large systems to be investigated by a suitable extension of conventional Monte Carlo methods. In the above-mentioned papers, the so-called Parallel Tempering algorithm was used. A well-performing implementation of the procedure, called Multi-Spin Coding, could be executed on general-purpose parallel computers. The outcome of this research gives strong support to the mean-field picture for EA spin glass. However, it is worth noting that interpreting the simulation outcomes is usually not trivial and only hints at the rigorous results. Most of all it calls for a further and deeper study of the behaviour of the realistic models of spin glasses.
Links:
1) http://www.claymath.org/millennium/P_vs_NP/
2) http://arxiv.org/abs/math/0309058
http://arxiv.org/abs/math-ph/0309063
http://arxiv.org/abs/math-ph/0407078
http://arxiv.org/abs/0807.1197
3) http://arxiv.org/abs/cond-mat/0503155
http://arxiv.org/abs/cond-mat/0510663
http://arxiv.org/abs/cond-mat/0607376
http://arxiv.org/abs/0902.0594
Please contact:
Pierluigi Contucci
Bologna University, Italy
E-mail:
Cristian Giardinà, Claudio Giberti, Cecilia Vernia
University of Modena and
Reggio Emilia, Italy
E-mail:










