by Alessandro Borri, Maria Domenica Di Benedetto and Giordano Pola
We present a general framework for the efficient synthesis of control algorithms enforcing complex logic specifications on Cyber-Physical Systems (CPS).
Cyber-Physical Systems (CPS) are attracting particular attention in the research and industrial communities given their impact on the future of Internet of Things, Systems of Systems, wearable electronics, brain-machine interaction and swarm systems, and other fields that require the integration of different, complementary competences. We focus on the role of control and in particular of Networked Control Systems (NCS) [1] and embedded control software synthesis [2] in building the foundations of CPS.
Particular emphasis is given in NCS to the non-idealities affecting communication among plants and controllers. The relevant ones are quantization errors, variable sampling/transmission intervals, time-varying delay in delivering messages through the network, limited bandwidth, packet dropouts, and scheduling protocols. Given the generality of the NCS model, results for the analysis and control design are difficult to obtain. Researchers, thus, typically focus only on subsets of these non-idealities. Results available in the literature mostly concern stability and stabilizability issues [1]. However, emerging requirements for CPS address different and perhaps more complex control objectives, for example: obstacle avoidance, synchronization specifications, enforcement of limit cycles and oscillatory behaviour.
The computer science community has developed methodologies for the control design of discrete systems with complex logic specifications. These techniques are general enough to address issues arising from CPS applications. However, this methodology cannot be directly applied to NCS, which include continuous dynamics. The focus of this article is an approach to deal with this class of systems by applying “correct-by-design embedded control software synthesis”.
Central to this approach is the construction of symbolic models, which are abstract descriptions of continuous systems where a symbol corresponds to an "aggregate" of continuous states. Once a symbolic model is constructed, which is equivalent to or approximates the original continuous dynamics, then the techniques developed for discrete models can be applied. Several classes of dynamical and control systems admit symbolic models, see for example [2] and the references therein.
In particular, we considered a general model of NCS comprising all the above mentioned non-idealities in the communication infrastructure. The proposed model is flexible enough to include other relevant features of CPS, such as specific communication protocols, data compression and encryption in the message delivery, and scheduling rules in the computing units. Under mild assumptions on the boundedness of the time-varying delays involved in the NCS, and of the incremental forward completeness on the plant, a symbolic model is constructed and proven to approximate the given NCS in the sense of alternating approximate simulation [2], for any desired accuracy. While being sound, this result exhibits the following drawback: if a controller, designed on the basis of the symbolic model for enforcing a given specification, fails to exist, there is no guarantee that a controller, enforcing the same specification, does not exist for the original NCS model. When alternating approximate simulation is replaced by alternating approximate bisimulation [2], the above drawback is overcome: we showed that if the plant of the NCS enjoys the stronger property of global asymptotic stability, a symbolic model can be constructed which approximates the NCS in the sense of alternating approximate bisimulation for any desired accuracy.
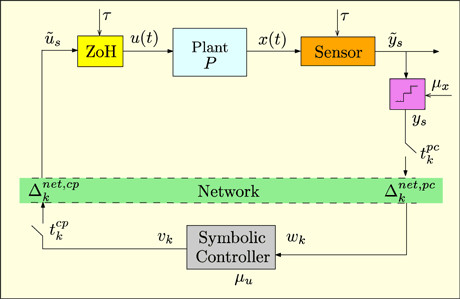
Figure 1: Example of control over networks in a cyber-physical system.
Once symbolic models are constructed, the symbolic control design of NCS can be addressed. We consider the following control problem: given a specification expressed in a fragment of Linear Temporal Logic, find a symbolic controller so that the closed-loop NCS system matches the specification with any desired accuracy. We solved this control problem by extending computer science results to metric transition systems. The resulting symbolic controller has been proven to be the approximate parallel composition of the symbolic model and of the specification. This approach is computationally intensive. We have developed efficient algorithms based on “on-the-fly” techniques to mitigate computational complexity.
The methodology proposed here is reported in detail in [3], which also includes an example of application of the techniques to the control design of a pair of nonlinear control systems sharing a common communication network. Since the requested symbolic controllers would exhibit a large space complexity (more than 1020 integers), we applied the aforementioned “on-the-fly” algorithm and designed symbolic controllers with a total space complexity of just 25,239 integers, still solving the original control problem. The closed-loop NCS obtained has been validated through the OMNeT++ network simulation framework, thus showing the effectiveness of the approach.
To the best of our knowledge, this is the first contribution where a general model of NCS is considered and where complex control problems are addressed. However these results are still theoretical and more work is needed to be relevant for industrial CPS.
Link: http://dews.univaq.it/
References:
[1] A. Bemporad et al. (Eds.): “Networked Control Systems”, LNCIS 406.
[2] P. Tabuada: “Verification and Control of Hybrid Systems: A Symbolic Approach”, Springer 2009.
[3] A. Borri et al.: “A symbolic approach to the design of nonlinear networked control systems”, HSCC’12.
Please contact:
Alessandro Borri,
IASI-CNR Biomathematics Laboratory, Rome, Italy
E-mail:
Maria Domenica Di Benedetto and Giordano Pola
University of L’Aquila, Italy.
E-mail: {mariadomenica.dibenedetto, giordano.pola} @univaq.it











