by Tarek Ahmed-Ali, Iasson Karafyllis and FrançoiseLamnabhi-Lagarrigue
Designing observers for nonlinear systems with communication constraints is a crucial challenge for Cyber-Physical Systems (CPS). Small gain techniques are used to derive new kinds of robust sampled-data observers for wide classes of nonlinear systems with delayed measurements.
The design of observers for systems with sampled and delayed measurements has been attracting increasing attention. The interest is greatly motivated by many industrial applications. From a practical viewpoint, an observer is a software sensor using a model and online measurements, and providing a real-time estimation of physical quantities which cannot be measured online. Those estimates can then be used for system control (dynamical output feedback) or monitoring (fault diagnosis). The most used observer algorithm is the famous Kalman filter, and its convergence is well established for linear systems. Its variant known as Extended Kalman Filter [1] can be used for nonlinear systems, but with the problems of gain tuning and stability guarantee. After the Luenberger [2] result for linear time-invariant systems, various other works have addressed this problem for nonlinear systems.
Two main approaches are described in the literature: one based on optimization, and one on analysis. In the latter approach, the most common idea is to characterize classes of systems which can be turned into another one, by change of variables (or immersion), allowing for a simpler observer design. The approach thus takes advantage of explicit structures, but remains dependent on the appropriate forms. Our work falls within this second approach. Very frequently we meet a system with: nonlinear characteristics, partial measurements, sampled measurements, measurements with errors, measurements with delays or uncertain sampling schedule. In fact, we rarely meet a system without one of these “annoying features”! The main question is then: How can we design a global exponential observer for such a system?
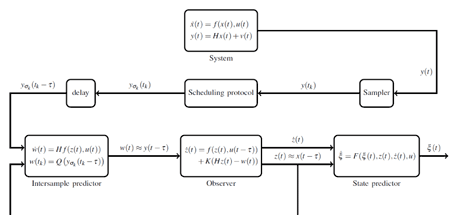
Figure 1: Structure of the observer z(t) given the system x(t).
Our team recently proposed new robust observers with respect to measurement errors and perturbations of the sampling schedule which use robust global exponential state predictors [3]. The global exponential sampled-data observers design is accomplished by using a small gain approach. Sufficient conditions are provided, which involve both the delay and the sampling period. The structure of the proposed observer, illustrated in Figure 1 can be described as follows:
- A hybrid sampled-data observer is first used in order to utilize the sampled and delayed measurements and provide an estimate of the delayed state vector,
- The estimate of the delayed state vector is used by the robust global exponential predictor. The predictor provides an estimate of the current value of the state vector.

Figure 2: The System

Figure 3: Designed observer z(t) for estimating online x(t).
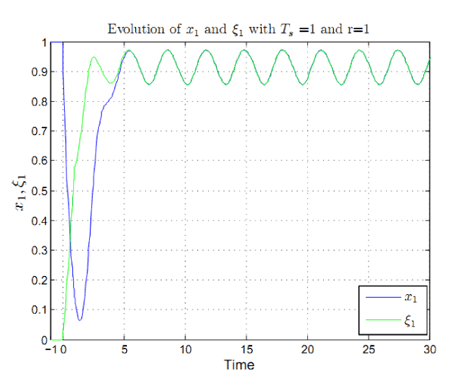
Figure 4: Time evolution of the first component of the observation error (x(t) – z(t)).
For example, for the system x(t) in Figure 2, the designed observer z(t) is given in Figure 3, and Figure 4 shows the exponential convergence of the observation error (x(t) – z(t)) to zero.
Future work will consider the application of recently proposed control schemes for which the input is delayed, the measurements are sampled and delayed and only an output is measured (the state vector is not available). These control schemes will consist of an observer for the delayed state vector, an inter-sample predictor for the output signal, an approximate predictor for the future value of the state vector and the nominal feedback law applied and computed for the predicted value of the future state vector.
References:
[1] R. E. Kalman: “A New Approach to Linear Filtering and Prediction Problems”, Transactions of the ASME - Journal of Basic Engineering, vol. 82, 1960, p. 35-45
[2] D. G. Luenberger: “An Introduction to Observers”, IEEE Transaction on Automatic Control, vol. 16, 1971, p. 596-602
[3] T. Ahmed-Ali, I. Karafyllis, F. Lamnabhi-Lagarrigue: “Global Exponential Sampled-Data Observers for Nonlinear Systems with Delayed Measurements”, Systems and Control Letters, 2013, 62(7) 539-549.
Please contact:
Tarek Ahmed-Ali Lagarrigue ENISICAEN-GREYC UMR 6072, France
E-mail:
Iasson Karafyllis, National Technical University of Athens, Greece
E-mail:
Françoise Lamnabhi-Lagarrigue CNRS-EECI SUPELEC, France
E-mail:











