by Thierry Colin, Angelo Iollo, Damiano Lombardi and Olivier Saut
Refractory thyroid carcinomas are a therapeutic challenge owing to some being fast-evolving - and consequently being good candidates for trials with molecular targeted therapies - whilst others evolve slowly. This variation makes it difficult to decide when to treat. In collaboration with Jean Palussière and Françoise Bonichon at the Institut Bergonié (regional centre for the fight against cancer), we have developed a diagnostic tool to help physicians predict the evolution of thyroidal lung nodules.
The evolution of thyroidal lung nodules may be difficult to evaluate. Furthermore, when unwell patients are concerned, physicians try to minimize the use of invasive techniques, restricting treatment (by radiofrequency ablation) to nodules that may become malignant. Thus, an accurate prognosis of each nodule is critical. We propose a numerical method of predicting the actual tumour growth for a specific patient.
Classically, accurate mathematical models describing tumoral growth involve a large number of parameters that cannot always be recovered from experimental data. The model proposed here is tuned for each patient thanks to two medical images following the evolution of a nodule. From this analysis, it is possible to obtain an estimate of the evolution of a targeted nodule using only non-invasive techniques.
Our model describes, not only the volume of the tumour, but also its localization and shape. It takes into account nutrient concentration, cell-cycle regulation and evolution of populations of cells, as well as mechanical effects. Our prediction relies on parameters estimation using temporal series of MRI or scans. The approach uses optimization techniques and Proper Orthogonal Decomposition (POD) to estimate the parameters of the chosen mathematical model (adapted to the type of cancer studied) that best fit with the real evolution of the tumour shown on the images.
Our model is a simplified Darcy-type model describing the evolution of various cellular densities (proliferative and quiescent cancer cells, healthy tissue…) as well as nutrients distribution or mechanical variables using Partial Differential Equations (PDE). This parametric model is sufficiently accurate to take into account the main physical features of tumor growth but simple enough to have its parameters recovered.
Essentially, the technique may be summarized as follows. Initially, the nodule under investigation is marked by the physicians on successive CT scans. From these images we recover the geometry of the lung and the shape of the nodule at different times. From the initial shape of the nodule, we run numerous numerical simulations of our mathematical model using a large set of parameter values. A basis using a POD approach is extracted from this large collection of numerical results. This time-consuming process can be efficiently performed on a High Performance Parallel Architecture since the direct simulations can be run concurrently and the POD extraction uses a parallel algorithm to be as fast as possible. The last step of the procedure consists in solving an inverse problem based on a Newton method to recover the parameters that best fit the available medical images of the nodule. Once these parameters are determined, a prediction is simply obtained by running the numerical code.

Figure 1: Evolution of the an untreated thyroidal nodule in the lung.

Figure 2: results of a prediction of the evolution of the nudule based on the mathematical model.
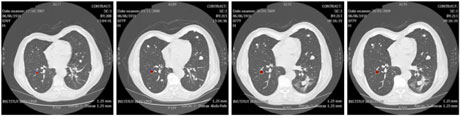
Figure 3: In addition to computing the volume of the tumour, the model can be used to predict the localization of the tumour (plotted in red).
We tested our technique on several test cases, one of which is presented in Figure 1. For a patient with an untreated thyroidal nodule in the lung, four computerised tomography (CT) scans were available (we show three of them illustrating the evolution of the nodule below).
We used the first two scans to perform the data assimilation and recover the parameters of the mathematical model adapted to the patient and to this nodule. Once these parameters are determined, the model is used in order to obtain predictions on the evolution of this nodule. The results of this prediction are plotted in Figure 2. The measured volume of the nodule from the CT scan is plotted using circles; the continuous line represents the volume computed using our tuned mathematical model.
Only the first two scans were used for data assimilation; the others are shown for the purpose of comparison. In addition to computing the volume of the tumour,our model enables usto predict its localization, as shown in the Figure 3 where the computed tumour is plotted in red.
For oncologists the development of such tools is of interest in therapy planning (and in the evaluation of an anti-tumoral treatment). For example a slowly evolving tumour prediction could reinforce the decision to wait without specific treatment. In the opposite case the simulation can support the decision to start a radiofrequency thermal ablation (for example) or a molecular targeted therapy.
Links:
INRIA Resarch Team MC2: http://www.math.u-bordeaux1.fr/MAB/mc2/
Institut Bergonié: http://www.bergonie.org/
Please contact:
Olivier Saut,
INRIA, France
Tel +33 5 40002115
E-mail:










