by Eszter Friedman, István Miklós and Jotun Hein
The Data Mining and Web Search Group at the SZTAKI in collaboration with the Genome Analysis and Bioinformatics Group at the Department of Statistics, University of Oxford, developed a Bayesian Markov chain Monte Carlo tool for analysing the evolution of metabolic networks.
"Nothing in biology makes sense except in the light of evolution". The famous quote by Theodosius Dobzhansky (1900-1975) has been the central thesis of comparative bioinformatics. In this field, the biological function, structure or rules are inferred by comparing entities (DNA sequences, protein sequences, metabolic networks, etc.) from different species. The observed differences between the entities can be used for predicting the underlying function, structure or rule that would be too expensive and laborious to infer directly in lab. These comparative methods have been very successful in silico approaches, for example, in protein structure prediction. The idea can be used for inferring metabolic networks, too.
Metabolic networks are under continuous evolution. Most organisms share a common set of reactions as a part of their metabolic networks that relate to essential processes. A large proportion of reactions present in different organisms, however, are specific to the needs of individual organisms or tissues. The regions of metabolic networks corresponding to these non-essential reactions are under continuous evolution. By comparing metabolic networks from different species, we can find out which parts of the metabolic network are essential (ie those that are common in all networks) and which are non-essential (ie those that are missing in at least one of the networks). Sometimes there is more than one possible metabolic network that can synthesise or degrade a specific chemical. These alternative solutions can be transformed into each other, and the ensemble of all possible reactions form a complicated network (see Figure 1).

Figure 1: The pentose phosphate pathway of Yersinia pseudotuberculosis strain YPIII. From the KEGG database, http://www.kegg.com
The central question is: what are the possible evolutionary pathways through which one metabolic network might evolve into another? This question is especially important to understand in the fight against drug-resistant bacteria. Drugs that are designed to protect us against illness-causing bacteria block an enzyme that catalyzes one of the reactions of the metabolic network of the bacteria. The bacteria, however, can avoid the effects of the drug by developing an alternative metabolic pathway. If we understand how the alternative pathways evolve we may be able to design a combination of drugs from which the bacteria cannot escape through the development of alternative pathways.
Analysis of past events is always coupled with some uncertainty about the nature and order of events that unfolded. It is therefore crucial to infer the evolution of metabolic networks using statistical methods that properly handle the uncertainty that inevitably occurs during analysis. Bayesian methods collect the a priori knowledge into an ensemble of distributions of random variables, set up a random model describing the changes, and calculate the posterior probabilities of what could happen. The relationship between the prior and posterior probabilities is described by the Bayes theorem as shown in Figure 2. Since the integral in the denominator is typically hard to calculate, and the Bayes theorem is often written in the form shown in Figure 3.
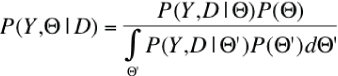
Figure 2: The relationship between the prior and posterior probabilities. D is the observed data (the metabolic networks), Y is the hidden data (the metabolic networks in the ancestral species that we cannot observe) and Θ is the set of parameters describing the evolution of metabolic networks (the rates with which the reactions of the network are deleted or inserted). P(Y, Θ | D) is the probability that the observed networks evolved from the set of networks Y in a mode described with parameters Θ. P(Y, D | Θ ) (called likelihood) is the probability that the random model with parameters Θ generates the observed and unobserved data, and P(Θ) is the prior distribution of the parameters.
![]()
Figure 3: Bayes theorem in the form as used in Bayesian statistics. Here µ stands for ‘proportional to’. The theorem is also used in a narrative form posterior µ likelihood x prior.
The Bayesian theorem in this form can be used in Monte Carlo methods to sample from the posterior distribution. The Markov chain Monte Carlo (MCMC) method sets up a Markov chain that converges to the desired distribution. After convergence, samples from the Markov chain follow the prescribed distribution.
MCMC Network implements the above-described Bayesian MCMC framework for inferring metabolic networks. We model the evolution of networks with a time-continuous Markov model. In this model, chemical reactions can be deleted from or inserted into the reaction network. Constraints such that the reaction network must be functioning after inserting or deleting a reaction are added to the model. The ??parameter set contains the insertion and deletion rates of the chemical reactions. We know a priori that the important parts of the reaction networks are usually compact parts of the network. The insertion and deletion rates on these important parts are smaller. We can express this knowledge with a Markovian Random Field (MRF) prior distribution. In MRF, the prior probability for a small insertion and deletion rate of a reaction is higher if the neighbour reactions also have small insertion and deletion rates. Our approach is the first implementation of a network evolution in which both the variation of insertion and deletion rates and correlation between the rates of neighbour chemical reactions are considered.
MCMC Network is not only the first implementation of a sophisticated model for chemical network evolution, it also has a user-friendly graphical interface. XML files downloaded from the Kyoto Encyclopedia of Genes and Genomes (http://www.kegg.com/) can be directly used as input files of the program. On the graphical interface, the users can monitor the progress of the Markov chain. The results of the analysis can be visualized on the graphical interface, and can also be saved as a text file for further analysis.
In the last decade, Bayesian methods have been extremely successful for analysing sequence evolution. The evolution of metabolic networks can now also be analysed within the Bayesian framework using our software. There is a continuous debate about the major governing rules in the evolution of networks. For example, it is still unclear which rules result in networks being scale-free. Our software is a useful tool for answering such questions.
Links:
MCMC Network: http://www.ilab.sztaki.hu/~feszter/mcmcNetwork/
KEGG database:http://www.kegg.com/
Data Mining and Web Search Group: http://datamining.sztaki.hu
Genome Analysis & Bioinformatics Group: http://www.stats.ox.ac.uk/research/genome
Please contact:
Eszter Friedman
SZTAKI, Hungary
Tel: +36 1 279 6172
E-mail:










