Is it worth trying to keep oneself informed? The answer seems obvious to any rational person, but is it really so? Imagine two companies making the same product. In setting their production levels, they face two conflicting factors: they would like to increase production in order to sell more of the product, but on the other hand, a larger supply means a lower price per unit.
Let us suppose that the more aggressive company announces its production level. We may think that the second company is then in a better position because it is able to adjust its production accordingly. Wrong! Moreover, it is actually better for the second company to avoid observing the production levels of the first, and in addition to make sure that the first one knows this. How this can be true? Can we justify or prove these statements? To do so, we must translate the problem into mathematics: that's when game theory enters.
We have two players, with their strategies being production levels and their payoffs as profits (revenue from product sales less production costs). The question is what they should do. How should they play? The fundamental concept is the Nash equilibrium - the assignment of strategies to players such that no one player can improve his payoff by changing only his own strategy. In the Nash equilibrium of the above game (the classic Stackelberg Duopoly), the profit of the first company is greater than that of the second, but the profit of the second company is increased if it does not know the production level of the first. Thus, it is better to be the first player, but if you are the second one you are better off not being informed.
There are many other socio-economic and biological processes involving interacting agents that can be modelled by game theory. Some of these problems have counterintuitive solutions, making it necessary to solve them mathematically or by numerical simulations rather than attempting to reason them out.
Cooperation between unrelated individuals in animal and human societies is an intriguing issue in biology and social sciences. This problem is described by the Prisoner's Dilemma, in which two players have two options: to cooperate or to defect. The game has a unique Nash equilibrium where both players defect. In fact, defection is the best response to both cooperation and defection of the opponent. However, both players are better off when they cooperate (see the payoff matrix in Figure 1).
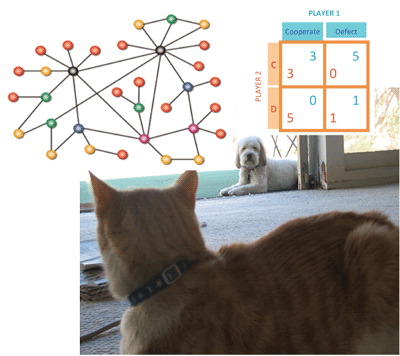
How can this social dilemma be solved? One solution is to interact not with everybody, but only with neighbours in your social network (which might look like the one in Figure 1). In this way many groups of linked cooperators are formed and are difficult to destroy. In spatial games, players are located on vertices of certain graphs and interact only with their neighbours. They may update their strategies using different dynamical rules such as best-reply or imitation. It has recently been observed that real social networks are of certain random types, the most popular being the Barabasi-Albert scale-free graph grown by a preferential attachment rule the greater the number of people to whom you are connected, the more likely you are to acquire a new colleague.
In a current project, 'Mathematical models of evolutionary game theory and genetic networks', supported by the grant from the Polish Ministry of Science and Higher Education and conducted in the Institute of Applied Mathematics, University of Warsaw, we study the long-run behaviour of spatial games, in particular the Prisoner's Dilemma on different networks. We observed for example that the density of cooperators undergoes abrupt changes with respect to various parameters in our models.
In many situations, multiple equilibria exist. We address the fundamental problem of equilibrium selection and study equilibrium transitions, using for example the methods and techniques of statistical physics. We explore the similarities and differences between socio-economic systems of interacting players and physical systems of interacting particles.
Networks themselves are formed as a result of the strategic choices of players. Moreover, in games on dynamic networks, agents may simultaneously choose their actions and co-players. We plan to investigate different approaches to the co-evolution of network structures and player strategies.
Link:
http://www.mimuw.edu.pl/~miekisz
Please contact:
Jacek Miękisz
Institute of Applied Mathematics and Mechanics, University of Warsaw, Poland
Tel: +48 22 5544469
E-mail: miekisz![]() mimuw.edu.pl
mimuw.edu.pl










