Optimal transportation problems arise in a variety of ways in everyday life. Originally formulated by Kantorovich as the problem of optimally transporting manufactured goods from their suppliers to some markets, it can also be studied in its measure theoretic version, where it corresponds to the problem of optimally moving a distribution of sand and rocks such that the surface flattens out. When the distributions considered are instead given by the time averages of two dynamical systems, the optimal cost is an abstract measure of the distance between their long-term dynamical behaviour. These time averages are computed from time series by way of a delay vector reconstruction, as is common in nonlinear time series analysis.
When computing the optimal cost, which is called the Wasserstein distance in the mathematical literature, the cost per unit of (probability) mass moved is proportional to the distance travelled. Numerically, the continuous problem is approximated by a discrete transportation problem, for which polynomial general-purpose algorithms exist. One direction for future research is the search for more efficient algorithms that make use of the special structure of the problem, i.e. that costs fulfil the triangle inequality. At the moment, the problem is further approximated by bootstrapping smaller subproblems from it, as the computations are otherwise too time consuming.
Residual Wasserstein Distances
Since we want to compare dynamical behaviour of physiological systems, the variability between subjects poses a serious problem. For example, if the amplitude of a parameter is different in two time series, is this due to anatomical differences or to a change in the dynamics? Since this is a priori unknown, it is not possible to simply normalize the time series.
We therefore defined the residual Wasserstein distances as optimal transportation distances where an initial translation and relative scaling of the two time averages incurs no cost. The resulting distances are scale-invariant and can be computed efficiently by an iterative majorization method, combined with the AUCTION algorithm due to Bertsekas. The latter starts from already computed solutions and relaxes them to optimal solutions of similar transportation problems. A software package for the statistical computing environment R has been developed which implements this method, and is available from the author's web page.
Dynamical Diseases
The concept of a dynamical disease has been defined by Milton & Mackey in a seminal paper as a change in the qualitative dynamics of a physiological control system when one or more parameters are changed. This idea allows the tools of nonlinear science to be applied in a clinical context as well, treating physiological processes as a noisy dynamical system. Diseases then correspond to parameter changes, leading to different long-term dynamical behaviour. The validity of this assumption has to be evaluated empirically.
Application to Breathing Data
An interesting application is the analysis of lung function, which is measured by superimposing an artificial pressure oscillation to the air and recording the integrated response of the lung. Two parameters were investigated from such forced oscillation recordings, characterizing the resistance and elasticity of the lung tissue. The dataset comprised twelve one-minute breathing measurements from 25 patients; it was supplied by P. J. Sterk and A. Slats and is described in full detail in their article published last year. Thirteen of the patients suffered from mild asthma and twelve from chronic obstructive pulmonary disease (COPD). These two lung diseases can be difficult to diagnose correctly when patients start to develop symptoms.
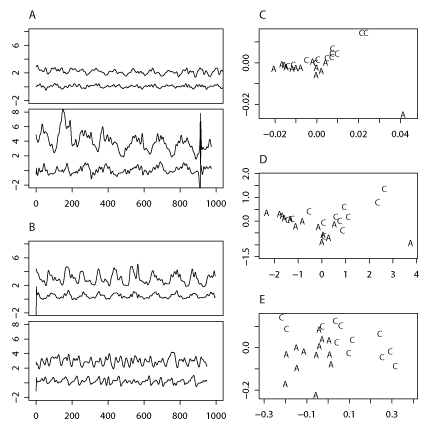
Figure 1 shows some of the original time series and two-dimensional representations of the computed distances. The latter are results obtained by residual Wasserstein distances (panel E) and two alternative methods, distances based on the means of the two parameters (panel D) and standard Euclidean distances between the time series (panel C).
Conclusions
The classification of lung diseases by residual Wasserstein distances is an interesting application of the concept of dynamical diseases and indeed allows better classification than by classical means. We are also investigating the possibility of tracking the progress of a disease by these distances, and the application of our method to different datasets, for example EEG or MEG brain recordings.
Link:
http://www.math.leidenuniv.nl/~muskulus
Please contact:
Michael Muskulus
Leiden University, The Netherlands
Tel: +31 71 527 7058
E-mail: muskulus![]() math.leidenuniv.nl
math.leidenuniv.nl










