Waves, although a source of delight, can apply significant and sometimes destructive pressure on coastal and urban areas, since their energy can grow enormously. Mathematical models account for such phenomena and offer a way of understanding how they form and propagate. Numerical discretization of such models provides tools to simulate existing observations and to forecast that which is yet to be seen and accounted for.
Free surface-water flow models provide the mathematics necessary to simulate flood waves. The full flow field, being turbulent and of geographical size, is described by the Navier-Stokes (NS) equations in complex 3D domains, supplied with appropriate turbulence closure models. The cascade of length and time scales therefore is huge, which makes the problem expressed in the Reynolds-Averaged (RANS) form computationally very demanding. Of particular difficulty is the discretization of the equations, the handling of the air-water interface movement and the poorly described turbulence characteristics. Recently, related research has been initiated in FORTH-IACM emphasizing high-resolution numerical techniques for the NS equations, in particular compact schemes and semi-implicit time-stepping.
A simpler yet reliable model is obtained by depth-averaging the NS equations using the shallow-water approximation. The water is considered to be an incompressible fluid with depth-averaged horizontal particle velocities, some variants as regards friction, and the Coriolis force (usually neglected). In addition, pressure is assumed to be hydrostatic, vertical accelerations negligible and depth-averaged viscous and turbulent stresses are applied. These are reasonable assumptions under the shallow-water hypothesis in many practical applications. As an alternative, the Bussinesq approximation is often used when dispersion is or is assumed to be relevant in modifying the waveforms. Such models are usually referred to as depth-averaged models. They provide qualitative approximate solutions efficiently and are therefore widely used in engineering applications.
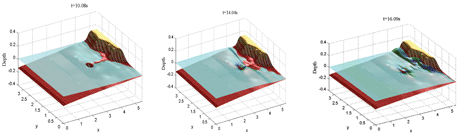
Due to the complex nature of the water motion, especially during the process of wave breaking, the numerical models used to simulate the run-up of breaking long waves must be treated meticulously. Related research at IACM-FORTH focuses on the development of finite-difference and finite-volume methods for solving the depth-averaged shallow-water equations on general 3D topographies, with special attention given to the modelling of shock (bore) waves and the generation of wet/dry fronts.
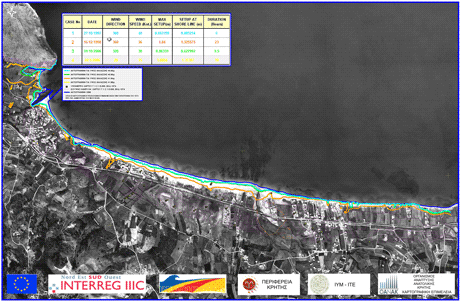
FORTH-IACM operates depth-averaged computational models (of shallow-water and Bussinesq type with emphasis on complex 3D domains) in the context of related EU projects. One of these is the TRANSFER project, which studies tsunami processes and hazard and risk assessment for the Mediterranean coast. Long waves are simulated by shallow-water simulation models coupled with in situ measurements and observations; the study of realistic scenarios is feasible and risk-reducing strategies can be developed. Another related project is the BEACHMEDe project, which focuses on the protection of the Mediterranean coastal zone from erosion and the implementation of evolving best practices to an observatory structure of the coastal zone. A major component of the project is to study the flooding of low coastal areas under extreme weather phenomena, and to use the associated flood maps in the civil planning of these areas.
Becoming familiar with observation and measurement techniques acquired in practice became an initiative for FORTH-IACM. It is hoped that investing in the development of relevant know-how will result in deeper insight into the wave phenomena under investigation and provide the means for major improvements in the reliability and effectiveness of existing simulation and forecasting models.
Please contact:
Nikolaos A. Kampanis
IACM-FORTH, Greece
E-mail: kampanis![]() iacm.forth.gr
iacm.forth.gr










