From the current growth rate of European immigration it is clear that in a few decades, people born outside Europe will represent a large percentage of the continent's total population. Although from an emotional point of view immigration is often perceived as a threat, to a large extent it represents an economic opportunity. When two cultures are merged, issues like the survival of each cultural identity play a major role in determining a proper and functional mutual integration. Historically there are several examples in which one cultural trait, despite being carried by only a small fraction of people, overcomes another in a relatively short time and with associated dramatic changes. In other cases, two different cultural traits may coexist peacefully for long periods of time.
Are we able to study these phenomena on solid scientific grounds? For instance, is it possible to establish what determines cultural robustness and what causes sudden changes from pre-existing cultural legacies? Can we predict or avoid such changes? From a modern epistemological perspective, can we build a 'simple' mathematical model that in terms of a few measurable parameters would provide a predictive description of the observed phenomenology at a social level?
Two research projects have taken on the challenge: a European team (CULTAPTATION) and a Strategic Team of University of Bologna . What is the idea the teams are hunting after? People interact, they exchange information, and within a given community they tend on average to imitate each other. While for a handful of people it is necessary to study all possible decision strategies, a million subjects have a well-defined social average status that is largely independent of individual details. The science that learnt how to infer the macroscopic properties of a large number of particles from rules governing mutual interaction of small groups is called statistical mechanics; it began with the work of Boltzmann and was used to derive the laws of thermodynamics. In recent decades a statistical mechanics formalism has proven to be an excellent method for studying typical problems in which a system is described by a large number of individuals and average properties are being investigated.
With this perspective, a statistical mechanics model has been introduced that aims to describe the interaction of two groups, for instance immigrants and residents. The model assumes that the elements of the two populations of sizes N1 and N2, with N=N1+N2 a very large number, interact within themselves with an interaction strength J1 in group 1 and J2 in group 2. Moreover a cross-group interaction with a tuneable strength Jint is present between individuals of different groups. The model is of mean-field type: it is assumed that individuals are nodes of a fully connected graph. By means of parameters that measure the strength of the interactions and by considering the original cultures prior to cultural meeting, it is possible to provide a quantitative description of the system. The model considered is rich of structure and able to predict, as the ratio N1/N of the population varies, not only the coexistence of cultures but also and especially sudden changes acting with the features of phase transitions. Figure 1 displays those occurrences.
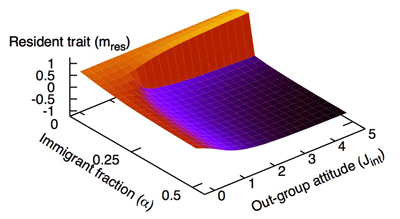
Future developments will evolve in two directions (I. Gallo, PhD thesis, in preparation). The first is to quantify the predictive value of the model by statistical estimation of parameters starting from poll data and using the maximum likelihood methods, thereby bridging theory and experiment. The second is to extend to realistic random interaction networks the formalism used so far. There is indeed clear evidence that the social interaction network among people exhibits several topological features that appear in random networks of 'small world' and 'scale-free' types. The necessity to extend the statistical mechanics methods to complex network environments is of fundamental importance. With this aim, the conference YEP-V addressed to Young European Probabilists has been organized by the authors. It was held in March 2008 at EURANDOM, Dutch institute member of EMS and ERCOM, to which one of the authors (C.G.) is affiliated. That initiative will continue and develop in a forthcoming conference at Banff International Research Station, Canada, in November 2009.
Links:
http://www.intercult.su.se/cultaptation/
http://www.dm.unibo.it/~contucci/sf.html
http://arxiv.org/abs/physics/0606062
http://arxiv.org/abs/physics/0702076
http://www.eurandom.tue.nl/workshops/2008/YEPV-r/YepVmain.htm
http://www.birs.ca/birspages.php?task=displayevent&event_id=09w5055
Please contact:
Pierluigi Contucci
Bologna University, Italy
Tel: +39 051 2094404
E-mail: contucci![]() dm.unibo.it
dm.unibo.it
Cristian Giardina
EURANDOM & TU/e, Eindhoven,
The Netherlands
Tel: +31 40 2472212
E-mail: c.giardina![]() tue.nl
tue.nl










