Inverse Problems: Making the Unseen Visible with Mathematics

The Finnish Centre of Excellence in Inverse Problem Research, funded by the Academy of Finland, was started in 2006. The centre comprises six research groups in Finnish universities, led by the inverse problem group at the Department of Mathematics and Statistics at the University of Helsinki. The centre's research is focused on developing the mathematical theory of inverse problems and solving inverse problems in a variety of applications, ranging in size from the molecular to the galactic level. The main goal is to build efficient and reliable mathematical models of targets even from very incomplete and noisy data, and this often results in the creation of images of entities that would otherwise remain unseen. Here we present a few examples.

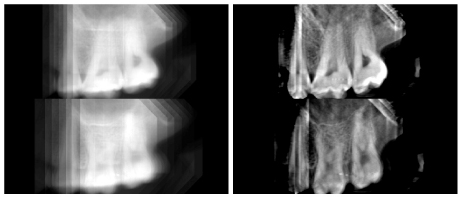
In medical imaging, more precise information is often needed about the 3D structure of a tissue than can be obtained with ordinary x-ray techniques. The detector records whether an x-ray was absorbed in its path through a tissue, but the images do not indicate the extent to which the x-ray was absorbed at particular points along its path. In other words, we are not able to determine depth of detail in the image. The 3D structure of a tissue can be determined by imaging the target from different directions and then mathematically computing the proportion of x-rays absorbed by the tissue at different points. This standard technique is used in computer tomography (CT). However, a disadvantage of CT is that it exposes the patient to high doses of radiation since many x-ray images are needed.

Statistical inversion techniques developed by our group alleviate this problem. By incorporating into the algorithm statistical a priori knowledge about the structure of interest, the number of images needed to calculate a reconstruction is significantly reduced. An example of this a priori knowledge is the positivity of the target function: tissue does not strengthen x-rays at any point. A priori knowledge of tissue differentiability is also frequently used in reconstruction calculations.

We are also developing a wholly different technique, called electrical impedance tomography, for viewing the insides of our body. This simple and inexpensive method is based on conducting very small currents through the body and measuring them on the surface: again, mathematics can turn such information into an actual image. The search for such a method also led to the solution of a long-standing hypothesis by Alberto Calderon.

Figure 1: (left) Two slices of a traditional x-ray image reconstruction of teeth; (right) the corresponding slices of a reconstruction made with our statistical inversion methods from the same raw data.

Figure 2: The reconstructed shape of asteroid 1862 Apollo, whose rotation speeds up due to sunlight.

We are also interested in solutions to geological and meteorological problems. The varying densities and materials below the surface of the Earth can be analysed with seismic imaging, and the bottoms of rivers or lakes can be accurately mapped with advanced sonar techniques. In the latter, we have developed pulse codes to pack as much information as possible into the transmitted and received sound signals, obtaining unprecedented spatial resolution. We use the same technique in radar experiments: with weather radar, for example, we are able to map the insides and the movements of regions of extreme weather with precision unattainable by traditional radar techniques.

In astronomy, too, our work finds application. Millions of asteroids in our solar system are seen only as points of light, even with the largest telescopes. Mathematics, however, makes it possible to reconstruct the rotation states and shapes of asteroids merely from brightness variations that can be recorded with small telescopes. The problem is to determine the shape of an object from the sizes of its projection-like quantities in different directions. We have shown that, contrary to the belief held for almost a century, this inverse problem of generalized projections can be solved. The solution is based on the fact that the object is not always illuminated and viewed from the same direction, ie we measure more than the sizes of its shadows. Related to this is a practical solution to the Minkowski problem: how can a polyhedron be reconstructed when only the areas and orientations of its facets are known?

Using this technique, it is now possible to carry out a comprehensive mapping of one of our solar system's least known regions, the asteroid belt. This method has also resulted in completely new discoveries, such as asteroid rotation powered by sunlight. This finding is the most internationally reported Finnish research result ever. We can directly see how the pressure of the photons slowly but surely influences the motion of asteroids. With this knowledge we can predict the motion of near-Earth objects more precisely, and may even be able to help avert a collision with the Earth.

Finally, just as an example that mathematics used in inverse problems cuts both ways: we have shown that with suitable optical materials it is mathematically possible to create optical wormholes. With such invisible tunnels, light can be transmitted from one site to another, without anyone seeing it between the two sites or even realising that there is a tunnel in the first place. With the engineering techniques of the future, this method can even be used in building appliances such as 3D televisions.

Links:
http://math.tkk.fi/inverse-coe
http://www.rni.helsinki.fi/~mjk
http://www.rni.helsinki.fi/~ljp
http://math.tkk.fi/~mjlassas/index.html.en

Please contact:
Mikko Kaasalainen
University of Helsinki, Finland
Tel: +358 9 19151441
E-mail: mikko.kaasalainenhelsinki.fi